
【题目】如图,在正方体ABCD﹣A1B1C1D1中,AB=2,点E是BC的中点. 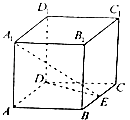
(1)求线段DE的长;
(2)求直线A1E与平面ADD1A1所成角的正弦值.
【答案】
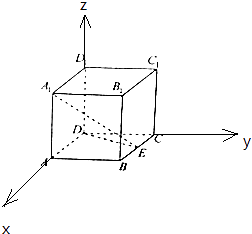
(1)解:以D为原点, ![]() ,
, ![]() ,
, ![]() 方向为x轴,y轴,z轴,建立空间直角坐标系,
方向为x轴,y轴,z轴,建立空间直角坐标系,
则D(0,0,0),E(1,2,0), ![]() =(1,2,0),
=(1,2,0),
∴线段DE的长| ![]() |=
|= ![]() =
= ![]() .
.
(2)解:∵A1(2,0,2),E(1,2,0),∴ ![]() =(﹣1,2,﹣2),
=(﹣1,2,﹣2),
∵平面ADD1A1的一个法向量 ![]() =(0,2,0),
=(0,2,0),
∴cos< ![]() ,
, ![]() >=
>= 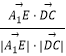 =
= ![]() =
= ![]() ,
,
∵直线A1E与平面ADD1A1所成角的正弦值等于 ![]() ,
,
∴直线A1E与平面ADD1A1所成角的正弦值为 ![]() .
.
【解析】(1)以D为原点, ![]() ,
, ![]() ,
, ![]() 方向为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出线段DE的长.(2)求出平面ADD1A1的一个法向量,利用向量法能求出直线A1E与平面ADD1A1所成角的正弦值.
方向为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出线段DE的长.(2)求出平面ADD1A1的一个法向量,利用向量法能求出直线A1E与平面ADD1A1所成角的正弦值.
【考点精析】解答此题的关键在于理解棱柱的结构特征的相关知识,掌握两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则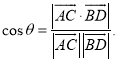 .
.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】大学生村官王善良落实政府“精准扶贫”精神,帮助贫困户张三用9万元购进一部节能环保汽车,用于出租.假设第一年需运营费用2万元,从第二年起,每年运营费用均比上一年增加2万元,该车每年的运营收入均为11万元.若该车使用了n(n∈N*)年后,年平均盈利额达到最大值,则n等于(注:年平盈利额=(总收入﹣总成本)× ![]() )( )
)( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() )x的图象与函数y=g(x)的图象关于直线y=x对称.
)x的图象与函数y=g(x)的图象关于直线y=x对称.
(1)若f(g(x))=6﹣x2 , 求实数x的值;
(2)若函数y=g(f(x2))的定义域为[m,n](m≥0),值域为[2m,2n],求实数m,n的值;
(3)当x∈[﹣1,1]时,求函数y=[f(x)]2﹣2af(x)+3的最小值h(a).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知P为△ABC所在平面外一点,PA⊥PB,PB⊥PC,PC⊥PA,PH⊥平面 ABC,H,则H为△ABC的( ) 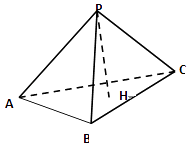
A.重心
B.垂心
C.外心
D.内心
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,关于正方体ABCD﹣A1B1C1D1 , 下面结论错误的是( ) 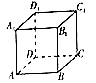
A.BD⊥平面ACC1A1
B.AC⊥BD
C.A1B∥平面CDD1C1
D.该正方体的外接球和内接球的半径之比为2:1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|ax﹣x2|+2b(a,b∈R).
(1)当a=﹣2,b=﹣ ![]() 时,解方程f(2x)=0;
时,解方程f(2x)=0;
(2)当b=0时,若不等式f(x)≤2x在x∈[0,2]上恒成立,求实数a的取值范围;
(3)若a为常数,且函数f(x)在区间[0,2]上存在零点,求实数b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com