
【题目】不等式![]() 对任意实数
对任意实数![]() 都成立,则实数
都成立,则实数![]() 的取值范围_________
的取值范围_________
【答案】![]()
【解析】
根据题意,分2种情况讨论:1°若a2﹣1=0,则a=±1,分别验证a=1或﹣1时,是否能保证该不等式满足对任意实数x都成立,
2°若a2﹣1≠0,不等式(a2﹣1)x2+(a﹣1)x﹣1≤0为二次不等式,结合二次函数的性质,解可得此时a的范围,综合可得答案.
根据题意,分2种情况讨论:
1°若a2﹣1=0,则a=±1,
当a=1时,不等式(a2﹣1)x2+(a﹣1)x﹣1≤0为:﹣1≤0,
满足对任意实数x都成立,则a=1满足题意,
当a=﹣1时,不等式(a2﹣1)x2+(a﹣1)x﹣1≤0为:﹣2x≤0,
不满足对任意实数x都成立,则a=﹣1不满足题意,
2°若a2﹣1≠0,不等式(a2﹣1)x2+(a﹣1)x﹣1≤0为二次不等式,
要保证(a2﹣1)x2+(a﹣1)x﹣1≤0对任意实数x都成立,
必须有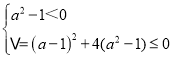 ,
,
解可得:![]() a<1,
a<1,
综合可得![]() a≤1,
a≤1,
故答案为:![]()


科目:高中数学 来源: 题型:
【题目】当生物死亡后,它机体内原有的碳14会按确定的规律衰减.按照惯例,人们将每克组织的碳14含量作为一个单位大约每经过5730年,一个单位的碳14衰减为原来的一半,这个时间称为“半衰期”.当死亡生物组织内的碳14的含量不足死亡前的千分之一时,用一般的放射性探测器就测不到碳14了.如果用一般的放射性探测器不能测到碳14,那么死亡生物组织内的碳14至少经过了_____个“半衰期”.(提示:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图①是一栋新农村别墅,它由上部屋顶和下部主体两部分组成.如图②,屋顶由四坡屋面构成,其中前后两坡屋面ABFE和CDEF是全等的等腰梯形,左右两坡屋面EAD和FBC是全等的三角形.点F在平面ABCD和BC上的射影分别为H,M.已知HM 5 m,BC 10 m,梯形ABFE的面积是△FBC面积的2.2倍.设∠FMH ![]()
![]() .
.
(1)求屋顶面积S关于![]() 的函数关系式;
的函数关系式;
(2)已知上部屋顶造价与屋顶面积成正比,比例系数为k(k为正的常数),下部主体造价与其 高度成正比,比例系数为16 k.现欲造一栋上、下总高度为6 m的别墅,试问:当![]() 为何值时,总造价最低?
为何值时,总造价最低?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)设函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,若函数
,若函数![]() 是
是![]() 上的单调增函数,求
上的单调增函数,求![]() 的值;
的值;
(3)是否存在一条直线与函数![]() 的图象相切于两个不同的点?并说明理由.
的图象相切于两个不同的点?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第18届国际篮联篮球世界杯将于2019年8月31日至9月15日在中国北京、广州等八座城市举行.届时,甲、乙、丙、丁四名篮球世界杯志愿者将随机分到![]() 、
、![]() 、
、![]() 三个不同的岗位服务,每个岗位至少有一名志愿者.
三个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人不在同一个岗位服务的概率;
(2)设随机变量![]() 为这四名志愿者中参加
为这四名志愿者中参加![]() 岗位服务的人数,求
岗位服务的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究变量![]() ,
,![]() 得到一组样本数据,进行回归分析,有以下结论
得到一组样本数据,进行回归分析,有以下结论
①残差平方和越小的模型,拟合的效果越好;
②用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小说明拟合效果越好;
越小说明拟合效果越好;
③线性回归方程对应的直线![]() 至少经过其样本数据点中的一个点;
至少经过其样本数据点中的一个点;
④若变量![]() 和
和![]() 之间的相关系数为
之间的相关系数为![]() ,则变量
,则变量![]() 和
和![]() 之间的负相关很强.
之间的负相关很强.
以上正确说法的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,用总长为定值l的篱笆围成长方形的场地,以墙为一边,并用平行于一边的篱笆隔开.

(1)设场地面积为y,垂直于墙的边长为x,试用解析式将y表示成x的函数,并确定这个函数的定义域;
(2)怎样围才能使得场地的面积最大?最大面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com