
【题目】高铁和航空的飞速发展不仅方便了人们的出行,更带动了我国经济的巨大发展.据统 计,在2018年这一年内从![]() 市到
市到![]() 市乘坐高铁或飞机出行的成年人约为
市乘坐高铁或飞机出行的成年人约为![]() 万人次.为了 解乘客出行的满意度,现从中随机抽取
万人次.为了 解乘客出行的满意度,现从中随机抽取![]() 人次作为样本,得到下表(单位:人次):
人次作为样本,得到下表(单位:人次):
满意度 | 老年人 | 中年人 | 青年人 | |||
乘坐高铁 | 乘坐飞机 | 乘坐高铁 | 乘坐飞机 | 乘坐高铁 | 乘坐飞机 | |
10分(满意) | 12 | 1 | 20 | 2 | 20 | 1 |
5分(一般) | 2 | 3 | 6 | 2 | 4 | 9 |
0分(不满意) | 1 | 0 | 6 | 3 | 4 | 4 |
(1)在样本中任取![]() 个,求这个出行人恰好不是青年人的概率;
个,求这个出行人恰好不是青年人的概率;
(2)在2018年从![]() 市到
市到![]() 市乘坐高铁的所有成年人中,随机选取
市乘坐高铁的所有成年人中,随机选取![]() 人次,记其中老年人出行的人次为
人次,记其中老年人出行的人次为![]() .以频率作为概率,求
.以频率作为概率,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)如果甲将要从![]() 市出发到
市出发到![]() 市,那么根据表格中的数据,你建议甲是乘坐高铁还是飞机? 并说明理由.
市,那么根据表格中的数据,你建议甲是乘坐高铁还是飞机? 并说明理由.
【答案】(1)![]() (2)分布列见解析,数学期望
(2)分布列见解析,数学期望![]() (3)建议甲乘坐高铁从
(3)建议甲乘坐高铁从![]() 市到
市到![]() 市.见解析
市.见解析
【解析】
(1)根据分层抽样的特征可以得知,样本中出行的老年人、中年人、青年人人次分别为![]() ,
,![]() ,
,![]() ,即可按照古典概型的概率计算公式计算得出;
,即可按照古典概型的概率计算公式计算得出;
(2)依题意可知![]() 服从二项分布,先计算出随机选取
服从二项分布,先计算出随机选取![]() 人次,此人为老年人概率是
人次,此人为老年人概率是![]() ,所以
,所以![]() ,即
,即![]() ,即可求出
,即可求出![]() 的分布列和数学期望;
的分布列和数学期望;
(3)可以计算满意度均值来比较乘坐高铁还是飞机.
(1)设事件:“在样本中任取![]() 个,这个出行人恰好不是青年人”为
个,这个出行人恰好不是青年人”为![]() ,
,
由表可得:样本中出行的老年人、中年人、青年人人次分别为![]() ,
,![]() ,
,![]() ,
,
所以在样本中任取![]() 个,这个出行人恰好不是青年人的概率
个,这个出行人恰好不是青年人的概率![]() .
.
(2)由题意,![]() 的所有可能取值为:
的所有可能取值为:![]()
因为在2018年从![]() 市到
市到![]() 市乘坐高铁的所有成年人中,随机选取
市乘坐高铁的所有成年人中,随机选取![]() 人次,此人
人次,此人
为老年人概率是![]() ,
,
所以![]() ,
,
![]() ,
,
![]() ,
,
所以随机变量![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
故![]() .
.
(3)答案不唯一,言之有理即可.
如可以从满意度的均值来分析问题,参考答案如下:
由表可知,乘坐高铁的人满意度均值为:![]()
乘坐飞机的人满意度均值为:![]()
因为![]() ,
,
所以建议甲乘坐高铁从![]() 市到
市到![]() 市.
市.


科目:高中数学 来源: 题型:
【题目】关于渐近线方程为![]() 的双曲线有下述四个结论:①实轴长与虚轴长相等,②离心率是
的双曲线有下述四个结论:①实轴长与虚轴长相等,②离心率是![]() ③过焦点且与实轴垂直的直线被双曲线截得的线段长与实轴长相等,④顶点到渐近线与焦点到渐近线的距离比值为
③过焦点且与实轴垂直的直线被双曲线截得的线段长与实轴长相等,④顶点到渐近线与焦点到渐近线的距离比值为![]() .其中所有正确结论的编号( )
.其中所有正确结论的编号( )
A.①②B.①③C.①②③D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了迎接2019年的高考,某学校进行了第一次模拟考试,其中五个班的考试成绩在500分以上的人数如下表,![]() 为班级,
为班级,![]() 表示500分以上的人数
表示500分以上的人数
| 1 | 2 | 3 | 4 | 5 |
| 20 | 25 | 30 | 30 | 25 |
(1)若给出数据,班级![]() 与考试成绩500以上的人数
与考试成绩500以上的人数![]() ,满足回归直线方程
,满足回归直线方程![]() ,求出该回归直线方程;
,求出该回归直线方程;
(2)学校为了更好的提高学生的成绩,了解一模的考试成绩,从考试成绩在500分以上1,3班学生中,利用分层抽样抽取5人进行调研,再从选中的5人中,再选3名学生写出“经验介绍”文章,则选的三名学生1班一名,3班2名的概率.
参考公式: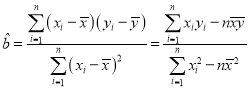 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗![]() 原料1千克、
原料1千克、![]() 原料2千克;生产乙产品1桶需耗
原料2千克;生产乙产品1桶需耗![]() 原料2千克,
原料2千克, ![]() 原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗
原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗![]() 原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是__________元.
原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是__________元.
查看答案和解析>>
科目:高中数学 来源: 题型:
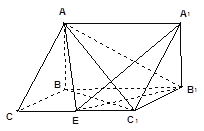
【题目】如图,在三棱柱![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() 侧面
侧面![]() .
.
(Ⅰ)求直线![]() 与底面
与底面![]() 所成角正切值;
所成角正切值;
(Ⅱ)在棱![]() (不包含端点)上确定一点E的位置,
(不包含端点)上确定一点E的位置,
使得![]() (要求说明理由);
(要求说明理由);
(Ⅲ)在(Ⅱ)的条件下,若![]() ,求二面角
,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C所对的边分别为a,b,c,已知asinB=bsin2A.
(1)求角A;
(2)若a=5,△ABC的面积为![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】波罗尼斯(古希腊数学家,约公元前262-190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽几乎使后人没有插足的余地.他证明过这样一个命题:平面内与两定点距离的比为常数k(![]() 且
且![]() )的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.现有
)的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.现有![]() ,
,![]() ,则当
,则当![]() 的面积最大时,AC边上的高为_______________.
的面积最大时,AC边上的高为_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com