
【题目】如图是某直三棱柱被削去上底后所得几何体的左视图、俯视图、直观图,在直观图中,M是BD的中点,左视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
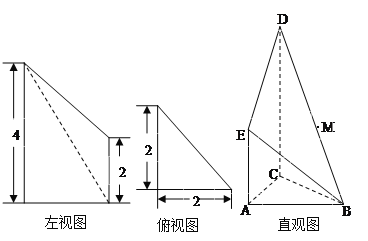
(Ⅰ)求该几何体的表面积和体积;
(Ⅱ)求点C到平面MAB的距离.
【答案】(Ⅰ)体积是4,表面积是![]() ; (Ⅱ)
; (Ⅱ)![]() .
.
【解析】试题分析:
(1)由题意得该几何体为四棱锥,然后根据三视图中的数据可得几何体的体积和表面积.(2)设C到面MAB的距离为![]() ,然后根据
,然后根据![]() 可得
可得![]() ,即所求的点到面的距离.
,即所求的点到面的距离.
试题解析:
由三视图可得,在几何体中,EA![]() 平面ABC,DC
平面ABC,DC![]() 平面ABC,AE∥DC,AE=2,DC=4,
平面ABC,AE∥DC,AE=2,DC=4,
AB![]() AC,且AC=2.
AC,且AC=2.
(Ⅰ)∵EA![]() 平面ABC,AB
平面ABC,AB![]() 平面ABC,
平面ABC,
∴EA![]() AB,
AB,
又AB![]() AC,
AC, ![]() ,
,
∴AB![]() 平面ACDE,
平面ACDE,
∴四棱锥B—ACDE的高![]() ,
,
又梯形ACDE的面积![]() ,
,
∴体积为![]() ;
;
表面积为S=![]()
![]()
![]() .
.
(Ⅱ)如图,过M作MN⊥BC于N,过N作NH⊥AB于H,则MH⊥AB.
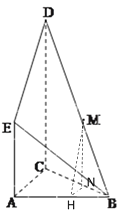
结合题意可得点M到AB的距离![]() ,
,
故![]() .
.
设C到面MAB的距离为![]() ,
,
由![]() 得:
得:
![]() ,
,
即![]()
解得![]() .即点C到平面MAB的距离
.即点C到平面MAB的距离![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如表1所示.
表1
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 17 | 8 | 25 |
学习积极性一般 | 5 | 20 | 25 |
合计 | 22 | 28 | 50 |
(1)如果随机从该班抽查一名学生,抽到积极参加班级工作的学生的概率是多少?抽到不积极参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法学生的学习积极性与对待班级工作的态度是否有关系?并说明理由.
参考表2
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
| 0.05 | 0.005 | 0.001 | ||
| 3.841 | 6.635 | 7.879 | 10.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况.
项目 员工 | A | B | C | D | E | F |
子女教育 | ○ | ○ | × | ○ | × | ○ |
继续教育 | × | × | ○ | × | ○ | ○ |
大病医疗 | × | × | × | ○ | × | × |
住房贷款利息 | ○ | ○ | × | × | ○ | ○ |
住房租金 | × | × | ○ | × | × | × |
赡养老人 | ○ | ○ | × | × | × | ○ |
(1)应从老、中、青员工中分别抽取多少人?
(2)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为A,B,C,D,E,F.享受情况如下表,其中“○”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
①试用所给字母列举出所有可能的抽取结果;
②设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一小袋中有3个红色、3个白色的乒乓球(其体积、质地完全相同),从袋中随机摸出3个球.
(1)求摸出的3个球都为白球的概率是多少?
(2)求摸出的3个球为2个红球、1个白球的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩(单位:分)如下:
公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩(单位:分)如下:
男:165 166 168 172 173 174 175 176 177 182 184 185 193 194
女:168 177 178 185 186 192
公司规定:成绩在180分以上(包括180分)者到“甲部门”工作;180分以下者到“乙部门”工作.
(1)求男生成绩的中位数及女生成绩的平均数.
(2)如果用分层随机抽样的方法从“甲部门”人选和“乙部门”人选中共选取5人,再从这5人中选2人,那么至少有一人是“甲部门”人选的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为提高学生学习的数学的兴趣,南京港师范大学附属中学拟开设《数学史》、《微积分先修课程》、《数学探究》、《数学建模》四门校本选修课程,甲、乙、丙三位同学打算在上述四门课程中随机选择一门进行学习,已知三人选择课程时互不影响,且每人选择每一门课程都是等可能的.
(1)求三位同学选择的课程互不相同的概率:
(2)求甲、乙两位同学不能选择同一门课程,求三人共有多少种不同的选课种数;
(3)若至少有两位同学选择《数学史》,求三人共有多少种不同的选课种数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com