
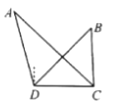
【题目】如图所示,为了测量A、B处岛屿的距离,小海在D处观测,A、B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶20海里至C处,观测B在C处的正北方向,A在C处的北偏西45°方向,则A、B两岛屿的距高为___________海里.
【答案】![]()
【解析】
如详解图,连接AB,在![]() 中,已知∠ACD=45°,∠ACD=45°,CD=20,可以由正弦定理求出AD 的边长,又在Rt△BCD中,已知∠BDC=45°,∠BCD=90°及CD=20长度此时可以求出AD=BD 再利用∠ADB=60°可以求出A、B两岛屿的距离.
中,已知∠ACD=45°,∠ACD=45°,CD=20,可以由正弦定理求出AD 的边长,又在Rt△BCD中,已知∠BDC=45°,∠BCD=90°及CD=20长度此时可以求出AD=BD 再利用∠ADB=60°可以求出A、B两岛屿的距离.

连接AB,由题意可知CD=20,∠ACD=45°,∠BDC=45°,∠BCD=90°,∠ACD=45°,∠CAD=30°,∠ADB=60°,
在△ACD中,由正弦定理得,![]()
∴AD=![]() ,
,
在Rt△BCD中,∵∠BDC=45°,∠BCD=90°,
∴BD=![]() CD=
CD=![]() .
.
在△ABD中,∠ADB=60°,AD=BD,所以,△ABD为等边三角形,所以,AB=![]() .
.


科目:高中数学 来源: 题型:
【题目】某商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客购物的相关数据如下表:
位顾客购物的相关数据如下表:
一次购物款(单位:元) |
|
|
|
|
|
顾客人数 |
|
|
|
|
|
统计结果显示![]() 位顾客中购物款不低于
位顾客中购物款不低于![]() 元的顾客占
元的顾客占![]() ,该商场每日大约有
,该商场每日大约有![]() 名顾客,为了增加商场销售额度,对一次购物不低于
名顾客,为了增加商场销售额度,对一次购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
(Ⅰ)试确定![]() ,
, ![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(Ⅱ)为了迎接春节,商场进行让利活动,一次购物款![]() 元及以上的一次返利
元及以上的一次返利![]() 元;一次购物不超过
元;一次购物不超过![]() 元的按购物款的百分比返利,具体见下表:
元的按购物款的百分比返利,具体见下表:
一次购物款(单位:元) |
|
|
|
|
返利百分比 |
|
|
|
|
请问该商场日均大约让利多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.![]() 为
为![]() 的右焦点,
的右焦点,![]() 为
为![]() 上一点,
上一点,![]() 轴,
轴,![]() 的半径为
的半径为![]() .
.
(1)求![]() 和
和![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点,其中
两点,其中![]() 在第一象限,是否存在
在第一象限,是否存在![]() 使
使![]() ?若存在,求
?若存在,求![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水库的蓄水量随时间而变化,现用t表示时间,以月为单位,年初为起点(用t表示第t月份,![]() ),根据历年数据,某水库的蓄水量V(单位:亿立方米)与时间t的近似函数关系为:当0<t≤10时,
),根据历年数据,某水库的蓄水量V(单位:亿立方米)与时间t的近似函数关系为:当0<t≤10时,![]() ;当10<t≤12时,
;当10<t≤12时,![]() ;若2月份该水库的蓄水量为33.6亿立方米.
;若2月份该水库的蓄水量为33.6亿立方米.
(1)求实数a的值;
(2)求一年内该水库的最大蓄水量.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]()
(1)若函数f(x)有两个零点,求实数a的取值范围;
(2)若a=3,且对任意的x1∈[-1,2],总存在![]() ,使g(x1)-f(x2)=0成立,求实数m的取值范围.
,使g(x1)-f(x2)=0成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“
为“![]() 类函数”.
类函数”.
(1)已知函数![]() ,试判断
,试判断![]() 是否为“
是否为“![]() 类函数”?并说明理由;
类函数”?并说明理由;
(2)设![]() 是定义在
是定义在![]() 上的“
上的“![]() 类函数”,求是实数
类函数”,求是实数![]() 的最小值;
的最小值;
(3)若
![]() 为其定义域上的“
为其定义域上的“![]() 类函数”,求实数
类函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了一款应用软件,为激发大家的学习兴趣,他们推出了“解数学题获取软件激活码”的活动,这款软件的激活码为下列数学问题的答案:已知数列1、1、2、1、2、4、8、1、2、4、8、16、……,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,再接下来的三项是
,再接下来的三项是![]() ,……,以此类推,求满足如下条件的最小整数
,……,以此类推,求满足如下条件的最小整数![]() 且该数列的前
且该数列的前![]() 项和为2的整数幂,那么该软件的激活码是________。
项和为2的整数幂,那么该软件的激活码是________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com