
【题目】如图,在棱长为1的正方体![]() 中,
中, ![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 上一动点.
上一动点.
(Ⅰ)求证:![]() ;
;
(Ⅱ)当![]() 时,求三棱锥
时,求三棱锥![]() 的体积;
的体积;
(Ⅲ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?说明理由.
?说明理由.
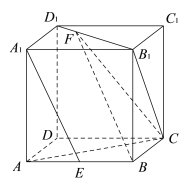
【答案】(1)证明见解析.
(2)![]() .
.
(3)存在;理由见解析.
【解析】
(1)连结![]() ,借助于正方体的特征,结合线面垂直的判定和线面垂直的性质,得到
,借助于正方体的特征,结合线面垂直的判定和线面垂直的性质,得到![]() ;
;
(2)根据题中的条件,确定出对应的点的位置,将三棱锥的顶点和底面转换,利用体积相等,求得结果;
(3)借助于平行四边形找到平行线,利用线面平行的判定定理,证得结果.
(Ⅰ)连结![]() .
.
在正方体![]() 中,
中,
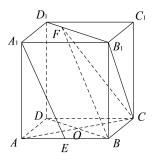
![]() ,
,![]() ,
,
所以![]() .
.
因为![]() 为正方形,
为正方形,![]() ,
,
所以![]() .
.
又因为![]() ,
,
所以![]() .
.
因为,
所以![]() .
.
(Ⅱ)过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .
.
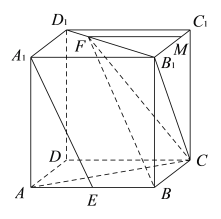
在正方体![]() 中,
中,
因为![]() ,
,
又因为![]() ,
,
所以![]() .
.
所以![]() 为三棱锥
为三棱锥![]() 的高.
的高.
因为![]() ,
,
所以![]() .
.
所以![]()
(III)存在. 当![]() 为
为![]() 中点时,
中点时,![]() 平面
平面![]() .
.
设![]() 为
为![]() 中点,连结
中点,连结![]() .
.
因为![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,
所以![]() .
.
因为![]() ,
,
所以![]() .
.
所以![]() .
.
在正方形![]() 中,
中,
因为![]() 为
为![]() 中点,
中点,
所以![]() ,且
,且![]() .
.
所以四边形![]() 为平行四边形.
为平行四边形.
所以![]()
因为![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.


科目:高中数学 来源: 题型:
【题目】定义非零向量![]() 的“相伴函数”为
的“相伴函数”为![]() (
(![]() ),向量
),向量![]() 称为函数
称为函数![]() 的“相伴向量”(其中
的“相伴向量”(其中![]() 为坐标原点),记平面内所有向量的“相伴函数”构成的集合为
为坐标原点),记平面内所有向量的“相伴函数”构成的集合为![]() .
.
(1)已知![]() (
(![]() ),求证:
),求证:![]() ,并求函数
,并求函数![]() 的“相伴向量”模的取值范围;
的“相伴向量”模的取值范围;
(2)已知点![]() (
(![]() )满足
)满足![]() ,向量
,向量![]() 的 “相伴函数”
的 “相伴函数”![]() 在
在![]() 处取得最大值,当点
处取得最大值,当点![]() 运动时,求
运动时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京市某年11月1日—20日监测最高最低温度及差值数据如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
最高温度(℃) | 20 | 16 | 14 | 20 | 20 | 20 | 18 | 15 | 12 | 11 | 12 | 12 | 13 | 9 | 8 | 6 | 13 | 11 | 10 | 14 |
最低温度(℃) | 5 | 4 | 2 | 4 | 9 | 6 | 9 | 3 | -1 | 0 | 5 | 1 | 4 | -1 | -4 | -2 | -1 | 0 | 1 | 3 |
差值(℃) | 15 | 12 | 12 | 16 | 11 | 14 | 9 | 12 | 13 | 11 | 7 | 11 | 9 | 10 | 12 | 8 | 14 | 11 | 9 | 11 |
(Ⅰ)完成下面的频率分布表及频率分布直方图,并写出频率分布直方图中![]() 的值;
的值;

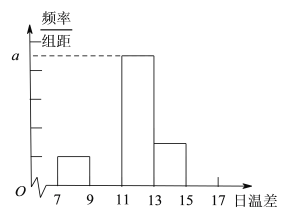
(Ⅱ)从日温差大于等于![]() 的这些天中,随机选取2天.求这两天中至少有一天的温差在区间
的这些天中,随机选取2天.求这两天中至少有一天的温差在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x∈(0, ![]() ),则函数f(x)=sinxtanx+cosxcotx的值域为( )
),则函数f(x)=sinxtanx+cosxcotx的值域为( )
A.[1,2)
B.[ ![]() ,+∞)
,+∞)
C.(1, ![]() ]
]
D.[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级有50名学生,其中有30名男生和20名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86,94,88,92,90,五名女生的成绩分别为88,93,93,88,93,下列说法正确的是( )
A.这种抽样方法是一种分层抽样
B.这种抽样方法是一种系统抽样
C.这五名男生成绩的方差大于这五名女生成绩的方差
D.该班男生成绩的平均数大于该班女生成绩的平均数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com