
【题目】设函数![]() .
.
(1)当![]() 时,试求
时,试求![]() 的单调增区间;
的单调增区间;
(2)试求![]() 在
在![]() 上的最大值;
上的最大值;
(3)当![]() 时,求证:对于
时,求证:对于![]() 恒成立.
恒成立.
【答案】(1) ![]() ;(2)详见解析; (3)详见解析.
;(2)详见解析; (3)详见解析.
【解析】试题分析:(1)当![]() 时,
时, ![]() ,
, ![]() ,当
,当![]() ,得
,得![]() ,所以
,所以![]() 的单调增区间为
的单调增区间为![]() ;(2)
;(2)![]() ,
, ![]() ,得
,得![]() ,讨论
,讨论![]() ,
, ![]() ,
, ![]() ,利用函数在区间
,利用函数在区间![]() 上的单调性可以求出函数
上的单调性可以求出函数![]() 在
在![]() 上的最大值;(3)当
上的最大值;(3)当![]() 时,设函数
时,设函数![]() ,则问题转化为证明对于
,则问题转化为证明对于![]() ,
, ![]() ,利用导数研究函数
,利用导数研究函数![]() 在区间
在区间![]() 的单调性,从而证明
的单调性,从而证明![]() 成立,于是问题得证.
成立,于是问题得证.
试题解析:(1)由![]() ,得
,得![]() .当
.当![]() 时,
时, ![]() ,令
,令![]() ,得
,得![]() .所以
.所以![]() 的单调增区间为
的单调增区间为![]() .
.
(2)令![]() ,得
,得![]() ,所以当
,所以当![]() 时,
时, ![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 单调递增;当
单调递增;当![]() 时,
时, ![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() 时,
时, ![]() ,
, ![]() 单调递减;
单调递减; ![]() 时,
时, ![]() ,
, ![]() 单调递增,综上,无论
单调递增,综上,无论![]() 为何值,当
为何值,当![]() 时,
时, ![]() 最大值都为
最大值都为![]() 或
或![]() .
. ![]() ,
,
![]() ,所以当
,所以当
![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() .
.
(3)令![]() ,所以
,所以![]() ,所以
,所以![]() ,令
,令![]() ,
,
解得![]() ,所以当
,所以当![]() 时,
时, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() 单调递增,所以当
单调递增,所以当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,所以
,所以![]() 恒成立.
恒成立.


科目:高中数学 来源: 题型:
【题目】为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出如图所示的频率分布直方图,已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在[100,120]之间的学生人数是( ) 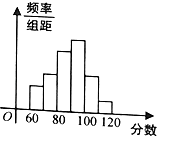
A.32
B.24
C.18
D.12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() 过点
过点![]() 且不与
且不与![]() 轴、
轴、![]() 轴垂直,且与圆
轴垂直,且与圆![]() 于
于![]() ,
, ![]() 两点,过
两点,过![]() 作
作![]() 的平行线交直线
的平行线交直线![]() 于点
于点![]() .
.
(1)证明![]() 为定值,并写出点
为定值,并写出点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 交
交![]() 于
于![]() 两点,过
两点,过![]() 且与
且与![]() 垂直的直线与圆
垂直的直线与圆![]() 交于
交于![]() 两点,求
两点,求![]() 与
与![]() 的面积之和的取值范围.
的面积之和的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(最大供应量)如表所示:
| 甲产品 | 乙产品 | 资源限额 |
煤(t) | 9 | 4 | 360 |
电力(kw·h) | 4 | 5 | 200 |
劳力(个) | 3 | 10 | 300 |
利润(万元) | 7 | 12 |
问:每天生产甲、乙两种产品各多少吨,获得利润总额最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位附近只有甲、乙两个临时停车场,它们各有![]() 个车位,为了方便市民停车,某互联网停车公司对这两个停车场,在某些固定时刻的剩余停车位进行记录,如下表:
个车位,为了方便市民停车,某互联网停车公司对这两个停车场,在某些固定时刻的剩余停车位进行记录,如下表:
时间 停车场 |
|
|
|
|
|
|
甲停车场 |
|
|
|
|
|
|
乙停车场 |
|
|
|
|
|
|
如果表中某一时刻剩余停车位数低于该停车场总车位数的![]() ,那么当车主驱车抵达单位附近时,该公司将会向车主发出停车场饱和警报.
,那么当车主驱车抵达单位附近时,该公司将会向车主发出停车场饱和警报.
(1)假设某车主在以上六个时刻抵达单位附近的可能性相同,求他收到甲停车场饱和警报的概率;
(2)从这六个时刻中任选一个时刻,求甲停车场比乙停车场剩余车位数少的概率;
(3)当乙停车场发出饱和警报时,求甲停车场也发出饱和警报的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=2,an+1﹣an﹣2n﹣2=0(n∈N*).
(1)求数列{an}的通项公式;
(2)设 ![]() ,若对任意的正整数n,当m∈[﹣1,1]时,不等式
,若对任意的正整数n,当m∈[﹣1,1]时,不等式 ![]() 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=3sin(ωx+φ)(ω>0,﹣![]() <φ<
<φ<![]() )的图象关于直线x=
)的图象关于直线x=![]() 对称,它的周期是π,则以下结论正确的个数( )
对称,它的周期是π,则以下结论正确的个数( )
(1)f(x)的图象过点(0,![]() )
)
(2)f(x)的一个对称中心是(![]() ,0)
,0)
(3)f(x)在[![]() ,
,![]() ]上是减函数
]上是减函数
(4)将f(x)的图象向右平移|φ|个单位得到函数y=3sinωx的图象.
A.4
B.3
C.2
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com