【题目】直线l过直线x+y﹣2=0和直线x﹣y+4=0的交点，且与直线3x﹣2y+4=0平行，求直线l的方程．
【答案】解：法一：联立方程： 
解得 
，即直线l过点（﹣1，3）， ∵直线l的斜率为 
，
∴直线l的方程为：y﹣3= （x+1），即3x﹣2y+9=0．
法二：∵直线x+y﹣2=0不与3x﹣2y+4=0平行，
∴可设直线l的方程为：x﹣y+4+λ（x+y﹣2）=0，
整理得：（1+λ）x+（λ﹣1）y+4﹣2λ=0．
∵直线l与直线3x﹣2y+4=0平行，
∴ 
，解得λ= 
，
∴直线l的方程为： 
x﹣ 
y+ 
=0，
即3x﹣2y+9=0．
【解析】解法一：联立方程，求得直线l经过的点的坐标，再利用点斜式求得直线l的方程．解法二：设直线l的方程为：x﹣y+4+λ（x+y﹣2）=0，再根据直线l与直线3x﹣2y+4=0平行，解得λ的值，可得直线l的方程．
科目：高中数学 来源： 题型：
【题目】若在曲线f（x，y）=0（或y=f（x））上两个不同点处的切线重合，则称这条切线为曲线f（x，y）=0或y=f（x）的“自公切线”．下列方程：
①x2﹣y2=1；
②y=x2﹣|x|；
③y=3sinx+4cosx；
④|x|+1= 
对应的曲线中存在“自公切线”的有（ ）
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=2cos2ωx+2sinωxcosωx（ω＞0）的最小正周期为π．
（1）求f（ 
）的值；
（2）求函数f（x）的单调递增区间．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4；坐标系与参数方程
在直角坐标系
中，直线
的参数方程为
（
为参数）．在以坐标原点为极点， 
轴正半轴为极轴的极坐标中，曲线
．
（Ⅰ）求直线
的普通方程和曲线
的直角坐标方程．
（Ⅱ）求曲线
上的点到直线
的距离的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知四棱锥P﹣ABCD的底面是矩形，侧面PAB是正三角形，且平面PAB⊥平面ABCD，E是PA的中点，AC与BD的交点为M．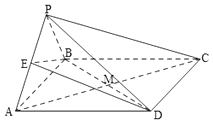 
（1）求证：PC∥平面EBD；
（2）求证：BE⊥平面AED．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一元二次不等式﹣x2+x+2＞0的解集是（ ）
A.{x|x＜﹣1或x＞2}
B.{x|x＜﹣2或x＞1}
C.{x|﹣1＜x＜2}
D.{x|﹣2＜x＜1}
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分13分）设关于
的一元二次方程
（
）有两根
和
，且满足
．
（1）试用表示
；
（2）求证：数列
是等比数列；
（3）当
时，求数列
的通项公式，并求数列
的前
项和
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若函数f（x）=ax2﹣（2a+1）x+a+1对于a∈[﹣1，1]时恒有f（x）＜0，则实数x的取值范围是（ ）
A.（1，2）
B.（﹣∞，1）∪（2，+∞）
C.（0，1）
D.（﹣∞，0）∪（1，+∞）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
