
【题目】已知函数f(x)=(λx+1)ln x-x+1.
(1)若λ=0,求f(x)的最大值;
(2)若曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直,证明:![]() >0.
>0.
【答案】见解析
【解析】(1)f(x)的定义域为(0,+∞),
当λ=0时,f(x)=ln x-x+1.
则f′(x)=![]() -1,令f′(x)=0,解得x=1.
-1,令f′(x)=0,解得x=1.
当0<x<1时,f′(x)>0,∴f(x)在(0,1)上是增函数;
当x>1时,f′(x)<0,∴f(x)在(1,+∞)上是减函数.
故f(x)在x=1处取得最大值f(1)=0.
(2)证明:由题可得,f′(x)=λln x+![]() -1.
-1.
由题设条件,得f′(1)=1,即λ=1.
∴f(x)=(x+1)ln x-x+1.
由(1)知,ln x-x+1<0(x>0,且x≠1).
当0<x<1时,f(x)=(x+1)ln x-x+1=xln x+(ln x-x+1)<0,
![]() >0.
>0.
当x>1时,f(x)=ln x+(xln x-x+1)=ln x-x![]() >0,∴
>0,∴![]() >0.
>0.
综上可知,![]() >0.
>0.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(-2,2),函数g(x)=f(x-1)+f(3-2x).
(1)求函数g(x)的定义域;
(2)若f(x)是奇函数,且在定义域上单调递减,求不等式g(x)≤0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届河北省衡水中学高三上学期六调】已知函数![]() ,其中
,其中![]() 均为实数,
均为实数,![]() 为自然对数的底数.
为自然对数的底数.
(1)求函数![]() 的极值;
的极值;
(2)设![]() ,若对任意的
,若对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的左焦点F为圆
的左焦点F为圆![]() 的圆心,且椭圆C上的点到点F的距离最小值为
的圆心,且椭圆C上的点到点F的距离最小值为![]() 。
。
(I)求椭圆C的方程;
(II)已知经过点F的动直线![]() 与椭圆C交于不同的两点A、B,点M坐标为(
与椭圆C交于不同的两点A、B,点M坐标为(![]() ),证明:
),证明: ![]() 为定值。
为定值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届陕西省西安市铁一中学高三上学期第五次模拟考试数学(文)】已知向量![]() ,
,![]() ,且函数
,且函数![]() .
.
(Ⅰ)当函数在![]() 上的最大值为3时,求
上的最大值为3时,求的值;
(Ⅱ)在(Ⅰ)的条件下,若对任意的![]() ,函数
,函数,![]() 的图像与直线
的图像与直线有且仅有两个不同的交点,试确定的值.并求函数在上的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(-x2+x-1)ex,其中e是自然对数的底数.
(1)求曲线f(x)在点(1,f(1))处的切线;
(2)若方程f(x)=![]() x3+
x3+![]() x2+m有3个不同的根,求实数m的取值范围.
x2+m有3个不同的根,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017兰州高考模拟】.在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形,AB∥DC,AB=AD=1,CD=2,AC=EC=![]() 。
。

(1)求证:平面EBC⊥平面EBD;
(2)设M为线段EC上一点,且3EM=EC,试问在线段BC上是否存在一点T,使得MT∥平面BDE,若存在,试指出点T的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某学科成绩(满分100分)是否与学生性别有关,采用分层抽样的方法,从高二年级抽取了30名男生和20名女生的该学科成绩,得到下图所示女生成绩的茎叶图.其中抽取的男生中有21人的成绩在80分以下,规定80分以上为优秀(含80分).

(1)请根据题意,将2×2列联表补充完整;
优秀 | 非优秀 | 总计 | |
男生 | |||
女生 | |||
总计 | 50 |
(2)据此列联表判断,是否有90%的把握认为该学科成绩与性别有关?
附: 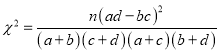 ,其中
,其中![]() .
.
参考数据 | 当 |
当 | |
当 | |
当 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com