
【题目】已知☉O:x2+y2=1和定点A(2,1),由☉O外一点P(a,b)向☉O引切线PQ,切点为Q,且满足|PQ|=|PA|.
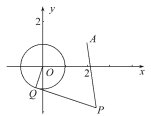
(1)求实数a,b间满足的等量关系.
(2)求线段PQ长的最小值.
(3)若以P为圆心所作的☉P与☉O有公共点,试求半径取最小值时☉P的方程.
【答案】(1) 2a+b-3= (2) ![]() (3) (x-
(3) (x-![]() )2+(y-
)2+(y-![]() )2=(
)2=(![]() -1)2
-1)2
【解析】(1)连接OP,
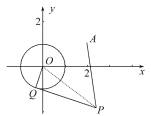
∵Q为切点,
∴PQ⊥OQ,
由勾股定理有|PQ|2=|OP|2-|OQ|2.
又由已知|PQ|=|PA|,故|PQ|2=|PA|2.
即(a2+b2)-12=(a-2)2+(b-1)2.
化简得实数a,b间满足的等量关系为:2a+b-3=0.
(2)方法一:由2a+b-3=0,得b=-2a+3.
|PQ|=![]() =
=![]()
=![]() =
=![]() .
.
故当a=![]() 时,|PQ|min=
时,|PQ|min=![]() .即线段PQ长的最小值为
.即线段PQ长的最小值为![]() .
.
方法二:由(1)知,点P在直线l:2x+y-3=0上.
∴|PQ|min=|PA|min,即求点A到直线l的距离.
∴|PQ|min=![]() =
=![]() .
.
(3)设☉P的半径为R,
∵☉P与☉O有公共点,☉O的半径为1,
∴|R-1|≤|OP|≤R+1.
即R≥||OP|-1|且R≤|OP|+1.
而|OP|=![]() =
=![]()
=![]() ,
,
故当a=![]() 时,|OP|min=
时,|OP|min=![]() .
.
此时,b=-2a+3=![]() ,Rmin=
,Rmin=![]() -1.
-1.
得半径取最小值时☉P的方程为(x-![]() )2+(y-
)2+(y-![]() )2=(
)2=(![]() -1)2.
-1)2.


科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当![]() 时,车流速度
时,车流速度![]() 是车流密度
是车流密度![]() 的一次函数.
的一次函数.
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)当车流密度![]() 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)![]() 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
⑴求函数![]() 的单调区间;
的单调区间;
⑵如果对于任意的![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
⑶设函数![]() ,
, ![]() .过点
.过点![]() 作函数
作函数![]() 的图象
的图象
的所有切线,令各切点的横坐标构成数列![]() ,求数列
,求数列![]() 的所有项之和
的所有项之和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种相互转化,相互统一的和谐美.定义:能够将圆![]() 的周长和面积同时等分成两部分的函数称为圆
的周长和面积同时等分成两部分的函数称为圆![]() 的一个“太极函数”.下列有关说法中:
的一个“太极函数”.下列有关说法中:

①对圆![]() 的所有非常数函数的太极函数中,一定不能为偶函数;
的所有非常数函数的太极函数中,一定不能为偶函数;
②函数![]() 是圆
是圆![]() 的一个太极函数;
的一个太极函数;
③存在圆![]() ,使得
,使得![]() 是圆
是圆![]() 的太极函数;
的太极函数;
④直线![]() 所对应的函数一定是圆
所对应的函数一定是圆![]() 的太极函数.
的太极函数.
所有正确说法的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
(1)当a<0时,判断f(x)在(0,+∞)上的单调性;
(2)当a=﹣4时,对任意的实数x1 , x2∈[1,2],都有f(x1)≤g(x2),求实数m的取值范围;
(3)当 ![]() ,
, 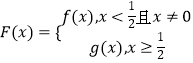 ,y=|F(x)|在(0,1)上单调递减,求a的取值范围.
,y=|F(x)|在(0,1)上单调递减,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在研究性学习中,收集到某制药厂今年前5个月甲胶囊生产产量(单位:万盒)的数据如下表所示:
| 1 | 2 | 3 | 4 | 5 |
| 1 | 4 | 5 | 6 | 6 |
(1)该同学为了求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,根据表中数据已经正确计算出
,根据表中数据已经正确计算出![]() ,试求出
,试求出![]() 的值,并估计该厂6月份生产的甲胶囊产量数;
的值,并估计该厂6月份生产的甲胶囊产量数;
(2)若某药店现有该制药厂今年二月份生产的甲胶囊4盒和三月份生产的甲胶囊5盒,小红同学从中随机购买了3盒甲胶囊.后经了解发现该制药厂今年二月份生产的所有甲胶囊均存在质量问题.记小红同学所购买的3盒甲胶囊中存在质量问题的盒数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com