Question

已知a，b，c，d是四条不重合的直线，其中c为a在平面α上的射影，d为b在平面α上的射影，则

1. A.
   a∥d?a∥b
2. B.
   a⊥b?c⊥d
3. C.
   a∥b?c∥d
4. D.
   c⊥d?a⊥b

Answer 1

C
分析：把四条直线均放在正方体ABCD-EFGH，然后取a=GH，d=BC，b=FD，满足要求a∥d，但推不出a∥b可以判断答案A错；
取a=BH，b=FD，C=BC，d=AD，满足要求a⊥b，但推不出c⊥d，可以判断答案B错；
因为斜线平行时，对应的射影要么平行，要么重合，要么为两个点，而题中交代a，b，c，d是四条不重合的直线，可以判断答案C对
取c=BC，d=AB，b=FB，a=BH，此时a，b所成角为60°，满足要求c⊥d，但推不出a⊥b，可以判断答案D错
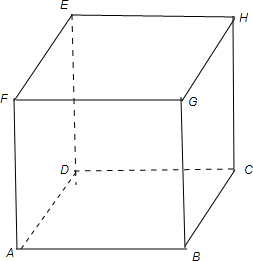
解答：解：把a，b，c，d这四条不重合的直线都放在正方体ABCD-EFGH中．
对于答案A：取a=GH，d=BC，b=FD，满足要求a∥d，但推不出a∥b，所以为假命题；
对于答案B：取a=BH，b=FD，C=BC，d=AD，满足要求a⊥b，但推不出c⊥d，所以为假命题；
对于答案C，因为斜线平行时，对应的射影要么平行，要么重合，要么为两个点，而题中交代a，b，c，d是四条不重合的直线，故射影平行，所以其为真命题；
对于答案D：取c=BC，d=AB，b=FB，a=BH，此时a，b所成角为60°，满足要求c⊥d，但推不出a⊥b，所以为假命题．
故选C．
点评：本题主要考查空间中直线和直线的位置关系．对于本题，由于a，b，c，d这四条不重合的直线可以任意摆放，直接想象就有难度，所以把它放在常见的正方体中，比较形象直观，这是本题做法中较好的地方．