
| A. | F>2 | B. | F≥2 | C. | F<2 | D. | F≤2 |
分析 先将方程化为标准方程;当方程表示圆的时候,$\frac{{D}^{2}{+E}^{2}-4F}{4}$=2-F>0,从而我们可以得出结论.
解答 解:圆方程化为标准方程为:(x+$\frac{D}{2}$)2+(y+$\frac{E}{2}$)2=$\frac{{D}^{2}{+E}^{2}-4F}{4}$,
∴-$\frac{D}{2}$=-1,D=2,-$\frac{E}{2}$=1,E=-2,
∴$\frac{{D}^{2}{+E}^{2}-4F}{4}$=2-F>0,
解得:F<2,
故选:C.
点评 圆的一般方程化为标准方程,可以知道圆的圆心与半径,同时也可知道方程表示圆的充要条件,属于中档题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:解答题
| 睡眠时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9] |
| 人数 | 2 | 4 | 8 | 4 | 2 |
| 睡眠时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9] |
| 人数 | 1 | 5 | 6 | 5 | 3 |
| 睡眠时间少于7小时 | 睡眠时间不少于7小时 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
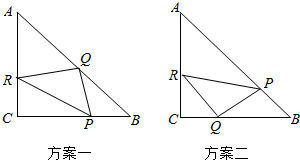 在一个直角边长为10m的等腰直角三角形ABC的草地上,铺设一个也是等腰直角三角形PQR的花地,要求P,Q,R三点分别在△ABC的三条边上,且要使△PQR的面积最小,现有两种设计方案:
在一个直角边长为10m的等腰直角三角形ABC的草地上,铺设一个也是等腰直角三角形PQR的花地,要求P,Q,R三点分别在△ABC的三条边上,且要使△PQR的面积最小,现有两种设计方案:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x>1,x2+1≤2 | B. | ?x>1,x2+1≤2 | C. | ?x≤1,x2+1≤2 | D. | ?x≤1,x2+1≤2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{10}$ | C. | 3$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com