
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x/年 | 3 | 5 | 6 | 7 | 9 |
| 推销金额y/万元 | 2 | 3 | 3 | 4 | 5 |
分析 (1)根据表中所给的5组数据,写出5个有序数对,画出平面直角坐标系,在坐标系中描出5个点,就是我们要求的散点图.
(2)首先求出x,y的平均数,利用最小二乘法做出b的值,再利用样本中心点满足线性回归方程和前面做出的横标和纵标的平均值,求出a的值,写出线性回归方程.
(3)第6名推销员的工作年限为11年,即当x=11时,把自变量的值代入线性回归方程,得到y的预报值,即估计出第6名推销员的年推销金额为5.9万元.
解答 解:(1)依题意,画出散点图如图所示,
(2)从散点图可以看出,这些点大致在一条直线附近,$\overline{x}$=6,$\overline{y}$=3.4,
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{5}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{5}({x}_{i}-\overline{x})^{2}}$=$\frac{10}{20}$=0.5,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=0.4,
∴年推销金额y关于工作年限x的线性回归方程为$\stackrel{∧}{y}$=0.5x+0.4.
(3)由(2)可知,当x=11时,
$\stackrel{∧}{y}$=0.5x+0.4=0.5×11+0.4=5.9(万元).
∴可以估计第6名推销员的年销售金额为5.9万元.
点评 本题考查回归分析的初步应用,考查利用最小二乘法求线性回归方程,是一个综合题目,这种题目非常符合新课标对于回归分析这一知识点的要求和考查思路.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
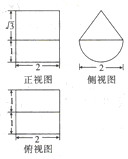
| A. | $2π+16+2\sqrt{3}$ | B. | $3π+16+2\sqrt{3}$ | C. | $3π+8+\sqrt{3}$ | D. | $3π+8+2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在空间四边形ABCD中,H,G分别是AD,CD的中点,E,F分别边AB,BC上的点,且$\frac{CF}{FB}$=$\frac{AE}{EB}$=$\frac{1}{3}$.求证:
在空间四边形ABCD中,H,G分别是AD,CD的中点,E,F分别边AB,BC上的点,且$\frac{CF}{FB}$=$\frac{AE}{EB}$=$\frac{1}{3}$.求证:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
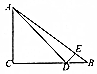 如图,在△ABC中,角A,B,C的对边分别为a,b,c,C=$\frac{π}{2}$,D,E分别为BC,AB上的点,∠ADC=∠EDB=$\frac{π}{4}$,DB=$\sqrt{2}$,AE=3EB,则边长AC的值为$\frac{3\sqrt{2}}{2}$.
如图,在△ABC中,角A,B,C的对边分别为a,b,c,C=$\frac{π}{2}$,D,E分别为BC,AB上的点,∠ADC=∠EDB=$\frac{π}{4}$,DB=$\sqrt{2}$,AE=3EB,则边长AC的值为$\frac{3\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | c>b>a | D. | b>a>c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com