已知△ABC的三个内角A、B、C的对边分别为a、b、c,且b2+c2=a2-bc,
(Ⅰ)求:2sinBcosC-sin(B-C)的值;
(Ⅱ)若b+c=2,设BC的中点为E,求线段AE长度的最小值.
解:(I)∵b
2+c
2=a
2-bc,∴a
2=b
2+c
2+bc,
结合余弦定理知cosA=

=

=-

,
又A∈(0,π),∴A=

∴B+C=

∴2sinBcosC-sin(B-C)=sinBcosC+cosBsinC
=sin(B+C)=sin

=

;
(II)根据题意知

=

(

+

)
∴
 2
2=

(
 2
2+
 2
2+2

•

)
∴

=

[c
2+b
2+2bc×(-

)]=

[(c+b)
2-3bc]=

(4-3bc)
∵

≤
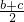
=1
∴bc≤1(当且仅当b=c=1时等号成立)
∴(
 2
2)
min=

(4-3)=

∴|
 |min
|min=

分析:(I)根据余弦定理表示出cosA,把已知得等式变形后代入即可求出cosA的值,由A的范围,利用特殊角的三角函数值即可求出A的度数,然后把所求的式子利用两角和与差的正弦函数公式及诱导公式化简,将sinA的值代入即可求出值;
(II)首先根据条件得出

=

(

+

)进而得出

=

(4-3bc),然后根据均值不等式得出bc≤1,即可求出结果.
点评:此题考查学生灵活运用余弦定理化简求值,灵活运用两角和与差的正弦函数公式化简求值,掌握正弦函数的值域,是一道中档题.

 =
= =-
=- ,
,

 =
= ;
; =
= (
( +
+ )
) 2=
2= (
( 2+
2+ 2+2
2+2 •
• )
) =
= [c2+b2+2bc×(-
[c2+b2+2bc×(- )]=
)]= [(c+b)2-3bc]=
[(c+b)2-3bc]= (4-3bc)
(4-3bc) ≤
≤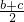 =1
=1 2)min=
2)min= (4-3)=
(4-3)=
 |min=
|min=
 =
= (
( +
+ )进而得出
)进而得出 =
= (4-3bc),然后根据均值不等式得出bc≤1,即可求出结果.
(4-3bc),然后根据均值不等式得出bc≤1,即可求出结果.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案