
【题目】2020年寒假是特殊的寒假,因为抗击疫情全体学生只能在家进行网上在线学习,为了研究学生在网上学习的情况,某学校在网上随机抽取120名学生对线上教育进行调查,其中男生与女生的人数之比为11∶13,其中男生30人对于线上教育满意,女生中有15名表示对线上教育不满意.
(1)完成![]() 列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
满意 | 不满意 | 总计 | |
男生 | 30 | ||
女生 | 15 | ||
合计 | 120 |
(2)从被调查的对线上教育满意的学生中,利用分层抽样抽取8名学生,再在8名学生中抽取3名学生,作线上学习的经验介绍,其中抽取男生的个数为![]() ,求出
,求出![]() 的分布列及期望值.
的分布列及期望值.
参考公式:附: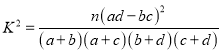
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 0.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10828 |
【答案】(1)表格见解析,有99%的把握认为对“线上教育是否满意与性别有关”;(2)分布列见解析,![]()
【解析】
(1)根据男生与女生的人数之比为11∶13,以及总人数120,可求出男,女生总人数,即可完成![]() 列联表,并根据独立性检验的基本思想,求出
列联表,并根据独立性检验的基本思想,求出![]() 的观测值,对照临界值表,即可判断是否有把握;
的观测值,对照临界值表,即可判断是否有把握;
(2)根据(1)可知,男生抽3人,女生抽5人,于是,离散型随机变量 的可能取值为![]() ,并且服从超几何分布,即可利用公式
,并且服从超几何分布,即可利用公式![]() (
(![]() ),求出各概率,得到分布列,求出期望
),求出各概率,得到分布列,求出期望
(1)因为男生人数为:![]() ,所以女生人数为
,所以女生人数为![]() ,
,
于是可完成![]() 列联表,如下:
列联表,如下:
满意 | 不满意 | 总计 | |
男生 | 30 | 25 | 55 |
女生 | 50 | 15 | 65 |
合计 | 80 | 40 | 120 |
根据列联表中的数据,得到![]() 的观测值
的观测值
![]() ,
,
所以有99%的把握认为对“线上教育是否满意与性别有关”.
(2)由(1)可知男生抽3人,女生抽5人,
依题可知![]() 的可能取值为
的可能取值为![]() ,并且
,并且![]() 服从超几何分布,
服从超几何分布,![]() (
(![]() ),即
),即
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
可得分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
可得![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,AD∥BC,BC=2AD,E,F分别为AD,BC的中点,AE=EF,![]() .将四边形ABFE沿EF折起,使平面ABFE⊥平面EFCD(如图2),G是BF的中点.
.将四边形ABFE沿EF折起,使平面ABFE⊥平面EFCD(如图2),G是BF的中点.
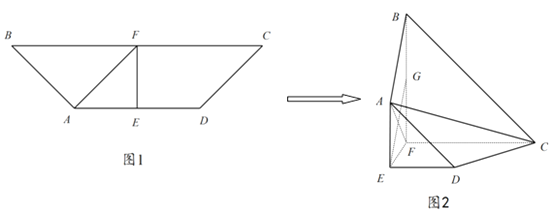
(1)证明:AC⊥EG;
(2)在线段BC上是否存在一点H,使得DH∥平面ABFE?若存在,求![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)求二面角D-AC-F的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对给定的d∈N*,记由数列构成的集合![]() .
.
(1)若数列{an}∈Ω(2),写出a3的所有可能取值;
(2)对于集合Ω(d),若d≥2.求证:存在整数k,使得对Ω(d)中的任意数列{an},整数k不是数列{an}中的项;
(3)已知数列{an},{bn}∈Ω(d),记{an},{bn}的前n项和分别为An,Bn.若|an+1|≤|bn+1|,求证:An≤Bn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,E、F分别为A1C1和BC的中点.
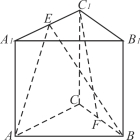
(1)求证:平面ABE⊥平面B1BCC1;
(2)求证:C1F//平面ABE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】未了解人们对“延迟退休年龄政策”的态度,某部门从年龄在15岁到65岁的人群中随机调查了100人,将这100人的年龄数据分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,整理得到如图所示的频率分布直方图.
,整理得到如图所示的频率分布直方图.
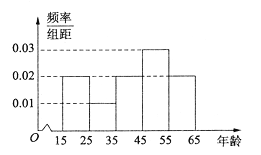
在这100人中不支持“延迟退休”的人数与年龄的统计结果如下:
年龄 |
|
|
|
|
|
不支持“延迟退休”的人数 | 15 | 5 | 15 | 23 | 17 |
(1)由频率分布直方图,估计这100人年龄的平均数;
(2)由频率分布直方图,若在年龄![]() ,
,![]() ,
,![]() 的三组内用分层抽样的方法抽取12人做问卷调查,求年龄在
的三组内用分层抽样的方法抽取12人做问卷调查,求年龄在![]() 组内抽取的人数;
组内抽取的人数;
(3)根据以上统计数据填写下面的![]() 列联表,据此表,能否在犯错误的概率不超过5%的前提下,认为以45岁为分界点的不同人群对“延迟退休年龄政策”的不支持态度存在差异?
列联表,据此表,能否在犯错误的概率不超过5%的前提下,认为以45岁为分界点的不同人群对“延迟退休年龄政策”的不支持态度存在差异?
\ | 45岁以下 | 45岁以上 | 总计 |
不支持 | |||
支持 | |||
总计 |
附:![]() ,其中
,其中![]() .
.
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com