
分析 由g(x)=ex-e2x的导数为ex-e2,求得单调区间和极值,画出y=f(x)的图象,求得方程的根,由题意可得y=f(x)与y=1-a有四个交点等价为0<1-a<e2,解不等式即可得到a的范围.
解答 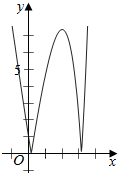 解:令g(x)=ex-e2x,则g′(x)=)=ex-e2,
解:令g(x)=ex-e2x,则g′(x)=)=ex-e2,
∴当x>2时,g′(x)>0,当x<2时,g′(x)<0,当x=2时,g′(x)=0,
∴当x>2时,g(x)是增函数;
当x<2时,g(x)是减函数减.
当x=2时g(x)取得极小值g(2)=-e2.
作出f(x)的函数图象如图:
令t=f(x),∵t2+at+a-1=0,
△=a2-4(a-1)=(a-2)2≥0,
∴t=-1或t=1-a,即f(x)=-1或f(x)=1-a,
∵f(x)≥0,∴f(x)=-1无解,
∵方程f2(x)+af(x)+a-1=0有四个不同的实数根,
∴f(x)=1-a有4个不同的实数根,
∴0<1-a<e2,解得1-e2<a<1.
故答案为(1-e2,1).
点评 本题考查函数和方程的转化思想,考查导数与单调区间和极值的关系,考查数形结合的思想方法,属于中档题.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 下列三个图分别是四棱锥A-BCEF的直观图、侧视图、俯视图,在直观图中,侧面ABC⊥底面BCEF,M为AC的中点,侧视图是等边三角形,俯视图是直角梯形,有关数据如图所示.
下列三个图分别是四棱锥A-BCEF的直观图、侧视图、俯视图,在直观图中,侧面ABC⊥底面BCEF,M为AC的中点,侧视图是等边三角形,俯视图是直角梯形,有关数据如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,AB⊥BC侧面PAB⊥底面ABCD,PA=AD=AB=2,BC=4,∠PAB=60°
在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,AB⊥BC侧面PAB⊥底面ABCD,PA=AD=AB=2,BC=4,∠PAB=60° 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com