
分析 可将f(x)变成:$f(x)=\frac{\frac{1}{x}-x}{[(\frac{1}{x}-x)^{2}+4]^{\frac{3}{2}}}$,可令$\frac{1}{x}-x=t$,并可求得t∈(0,+∞),并设y=f(x),从而得到y=$\frac{t}{({t}^{2}+4)^{\frac{3}{2}}}$,通过求导,根据导数符号即可得出t取何值时,函数y取到最大值,求出该最大值即可.
原不等式可变成$\frac{1}{\sqrt{\frac{1}{{x}^{2}}+1}}-\frac{2}{\frac{1}{{x}^{2}}+1}+1>0$,可令$\frac{1}{\sqrt{\frac{1}{{x}^{2}}+1}}=t$,并可根据x的范围求出t的范围,并且得到不等式-2t2+t+1>0,解出该不等式,再把所得t的范围和前面t的范围求交集,这样便可得出原不等式的解集.
解答 解:$f(x)=\frac{{x}^{2}-{x}^{4}}{(1+{x}^{2})^{3}}=\frac{\frac{1}{x}-x}{(\frac{1}{x}+x)^{3}}$=$\frac{\frac{1}{x}-x}{[(\frac{1}{x}+x)^{2}]^{\frac{3}{2}}}$=$\frac{\frac{1}{x}-x}{[(\frac{1}{x}-x)^{2}+4]^{\frac{3}{2}}}$;
设$\frac{1}{x}-x=t$,$t′=-\frac{1}{{x}^{2}}-1<0$,∴函数t=$\frac{1}{x}-x$在(0,1)上为减函数;
∴t>0;
设y=f(x),则y=$\frac{t}{({t}^{2}+4)^{\frac{3}{2}}}$$y′=\frac{2({t}^{2}+4)^{\frac{1}{2}}(2-{t}^{2})}{({t}^{2}+4)^{3}}$;
∴$t∈(0,\sqrt{2})$时,y′>0,t$∈(\sqrt{2},+∞)$时,y′<0;
∴$t=\sqrt{2}$时,y取最大值$\frac{\sqrt{2}}{{6}^{\frac{3}{2}}}=\frac{\sqrt{3}}{18}$;
∴f(x)的最大值为$\frac{\sqrt{3}}{18}$;
由原不等式得:$\frac{1}{\sqrt{\frac{1}{{x}^{2}}+1}}+\frac{\frac{1}{{x}^{2}}+1-2}{\frac{1}{{x}^{2}}+1}>0$;
∴$\frac{1}{\sqrt{\frac{1}{{x}^{2}}+1}}-\frac{2}{\frac{1}{{x}^{2}}+1}+1>0$;
令$\frac{1}{\sqrt{\frac{1}{{x}^{2}}+1}}=t$,$0<t<\frac{\sqrt{2}}{2}$;
∴得到-2t2+t+1>0;
解得$-\frac{1}{2}<t<1$,又$0<t<\frac{\sqrt{2}}{2}$;
∴$0<t<\frac{\sqrt{2}}{2}$;
∴x∈(0,1);
∴原不等式的解集为(0,1).
故答案为:$\frac{\sqrt{3}}{18},(0,1)$.
点评 考查将函数解析式变形,然后换元,从而求原函数最值的方法,根据导数符号判断函数单调性的方法,以及根据导数求函数最值的方法及过程,将不等式变形,然后换元,然后解换元后不等式,从而解出原不等式的方法.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
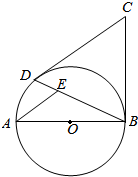 如图,切线CD、CB分别与⊙O相交于点D、B,AB为⊙O的直径,AE∥CD交BD于点E,若AB=BC,则sin∠BAE的值为$\frac{3}{5}$.
如图,切线CD、CB分别与⊙O相交于点D、B,AB为⊙O的直径,AE∥CD交BD于点E,若AB=BC,则sin∠BAE的值为$\frac{3}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{16}$ | B. | $\frac{π}{8}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com