
【题目】某品牌汽车4S店,对该品牌旗下的A型、B型、C型汽车进行维修保养,汽车4S店记录了100辆该品牌三种类型汽车的维修情况,整理得下表:
车型 | A型 | B型 | C型 |
频数 | 20 | 40 | 40 |
假设该店采用分层抽样的方法从上述维修的100辆该品牌三种类型汽车中随机取10辆进行问卷回访.
(1)求A型、B型、C型各车型汽车抽取的数目;
(2)维修结束后这100辆汽车的司机采用“100分制”打分的方式表示对4S店的满意度,按照大于等于80为优秀,小于80为合格,得到如下列联表:
优秀 | 合格 | 合计 | |
男司机 | 10 | 38 | 48 |
女司机 | 25 | 27 | 52 |
合计 | 35 | 65 | 100 |
问能否在犯错误概率不超过0.01的前提下认为司机对4S店满意度与性别有关系?请说明原因.
(参考公式: )
)
附表:
| 0.100 | 0.050 | 0.010 | 0.001 |
K | 2.706 | 3.841 | 6.635 | 10.828 |
科目:高中数学 来源: 题型:
【题目】“![]() 猜想”是指对于每一个正整数
猜想”是指对于每一个正整数![]() ,若
,若![]() 为偶数,则让它变成
为偶数,则让它变成![]() ;若
;若![]() 为奇数,则让它变成
为奇数,则让它变成![]() .如此循环,最终都会变成
.如此循环,最终都会变成![]() ,若数字
,若数字![]() 按照以上的规则进行变换,则变换次数为偶数的频率是( )
按照以上的规则进行变换,则变换次数为偶数的频率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,是由矩形![]() ,
,![]() 和
和![]() 组成的一个平面图形,其中
组成的一个平面图形,其中![]() ,
,![]() ,将其沿
,将其沿![]() 折起使得
折起使得![]() 重合,连接
重合,连接![]() 如图②.
如图②.
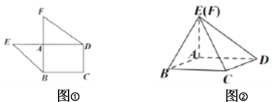
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为线段
为线段![]() 中点,求直线
中点,求直线![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知圆![]() ,圆
,圆![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切并且与圆
外切并且与圆![]() 内切,圆心
内切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)![]() 是与圆
是与圆![]() ,圆
,圆![]() 都相切的一条直线,
都相切的一条直线,![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,当圆
两点,当圆![]() 的半径最长时,求
的半径最长时,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房产销售公司从登记购房的客户中随机选取了50名客户进行调查,按他们购一套房的价格(万元)分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 得到频率分布直方图如图所示.用频率估计概率.
得到频率分布直方图如图所示.用频率估计概率.
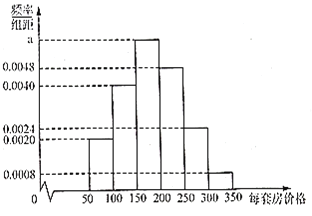
房产销售公司每卖出一套房,房地产商给销售公司的佣金如下表(单位:万元):
房价区间 |
|
|
|
|
|
|
佣金收入 | 1 | 2 | 3 | 4 | 5 | 6 |
(1)求![]() 的值;
的值;
(2)求房产销售公司卖出一套房的平均佣金;
(3)若该销售公司平均每天销售4套房,请估计公司月(按30天计)利润(利润=总佣金-销售成本).
该房产销售公司每月(按30天计)的销售成本占总佣金的百分比按下表分段累计/span>计算:
月总佣金 | 不超过100万元的部分 | 超过100万元至200万元的部分 | 超过200万元至300万元的部分 | 超过300万元的部分 |
销售成本占 佣金比例 |
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com