
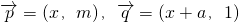 ,二次函数
,二次函数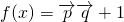 ,关于x的不等式f(x)>(2m-1)x+1-m2的解集为(-∞,m)∪(m+1,+∞),其中m为非零常数,设
,关于x的不等式f(x)>(2m-1)x+1-m2的解集为(-∞,m)∪(m+1,+∞),其中m为非零常数,设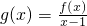 .
.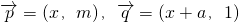 ,
,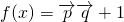 ,
,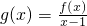 =
= ,
,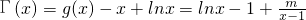 ,
,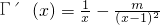 ,
,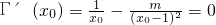
 ,
, (x>2),
(x>2),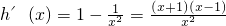 ,
, ,∴
,∴ 在(2,+∞)上为增函数,
在(2,+∞)上为增函数, ,
,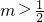 .
.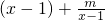 -kln(x-1)的定义域为(1,+∞).
-kln(x-1)的定义域为(1,+∞).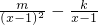 =
=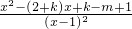 .
.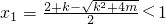 ,
, ,
, 时,x2-(2+k)x+k-m+1≥0恒成立,φ'(x)≥0,φ(x)在(1,+∞)上为增函数,
时,x2-(2+k)x+k-m+1≥0恒成立,φ'(x)≥0,φ(x)在(1,+∞)上为增函数,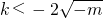 或
或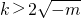 ,
,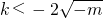 ,则
,则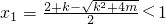 ,
,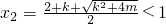 ,
,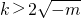 时,
时, ,
, ,
,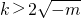 时,函数φ(x)有极大值和极小值,
时,函数φ(x)有极大值和极小值,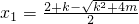 ,
,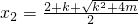 .
.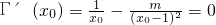
 ;由切点的横坐标x0满足|x0-1|+x0>3,可得x0>2.令
;由切点的横坐标x0满足|x0-1|+x0>3,可得x0>2.令 (x>2),利用导数可得其单调性,即可得到m的取值范围;
(x>2),利用导数可得其单调性,即可得到m的取值范围;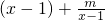 -kln(x-1)的定义域为(1,+∞).可得φ'(x)=1-
-kln(x-1)的定义域为(1,+∞).可得φ'(x)=1-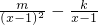 =
=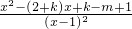 .方程x2-(2+k)x+k-m+1=0(*)的判别式△=(2+k)2-4(k-m+1)=k2+4m.通过对△和m分类讨论即可得出.
.方程x2-(2+k)x+k-m+1=0(*)的判别式△=(2+k)2-4(k-m+1)=k2+4m.通过对△和m分类讨论即可得出.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
| 2x2+(a-10)x+5 | f(x) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 2x2+(a-10)x+5 |
| f(x) |
查看答案和解析>>
科目:高中数学 来源:河北省正定中学2010届高三上学期第一次月考(理) 题型:解答题
已知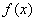 是二次函数,不等式
是二次函数,不等式 的解集为
的解集为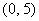 ,且
,且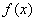 在区间
在区间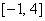 上的最大值为12.
上的最大值为12.
(1)求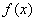 的解析式;
的解析式;
(2)解关于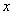 的不等式
的不等式 .
.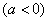
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com