练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

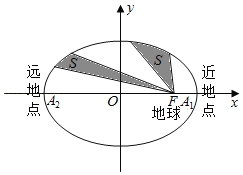
    【题目】人造地球卫星绕地球运行遵循开普勒行星运动定律:如图，卫星在以地球的中心为焦点的椭圆轨道上绕地球运行时，其运行速度是变化的，速度的变化服从面积守恒规律，即卫星的向径(卫星与地心的连线)在相同的时间内扫过的面积相等设该椭圆的长轴长、焦距分别为，.某同学根据所学知识，得到下列结论:

    ①卫星向径的取值范围是

    ②卫星向径的最小值与最大值的比值越大，椭圆轨道越扁

    ③卫星在左半椭圆弧的运行时间大于其在右半椭圆弧的运行时间

    ④卫星运行速度在近地点时最小，在远地点时最大

    其中正确的结论是（ ）

    A.①②B.①③C.②④D.①③④

    【答案】B

    【解析】

    ①根据椭圆的简单几何性质可知卫星向径的最小值和最大值分别为什么；

    ②根据向径的最小值与最大值的比值，结合椭圆的性质即可得出结论；

    ③根据在相同的时间内扫过的面积相等，即可判断

    ④根据题意结合椭圆的图形知卫星运行速度在近地点时最大，在远地点时最小．

    解：如图所示，

    对于①，卫星向径的最小值为，最大值为，①正确；

    对于②，卫星向径的最小值与最大值的比值为，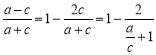

    越小，就越大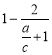，就越小，椭圆轨道越扁，②错误；

    对于③，根据在相同的时间内扫过的面积相等，卫星在左半椭圆弧的运行时间大于其在右半椭圆弧的运行时间，③正确；

    对于④，卫星运行速度在近地点时最大，在远地点时最小，④错误；

    综上，正确结论的序号是①③，共2个．

    故选．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在平行四边形中，，，.

    （1）求点的坐标；

    （2）过点的直线与平行四边形围成的区域（包括边界）有公共点，求直线的倾斜角的取值范围；

    （3）对角线所在的直线与圆：没有交点，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右焦点分别为

    （1）求以椭圆C的焦点为顶点，顶点为焦点的椭圆方程；

    （2）过椭圆C的左焦点且倾斜角为的直线与椭圆交于A,B两点，求的面积；

    （3）过定点的直线交椭圆C于AB两点，求弦AB中点P的轨迹方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆 的长轴长为4，焦距为

    （Ⅰ）求椭圆的方程；

    （Ⅱ）过动点的直线交轴与点，交于点 (在第一象限)，且是线段的中点.过点作轴的垂线交于另一点，延长交于点.

    （ⅰ）设直线的斜率分别为，证明为定值；

    （ⅱ）求直线的斜率的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在梯形ABCD中，AB∥CD，AD＝DC＝CB＝1，∠BCD＝120°，四边形BFED为矩形，平面BFED⊥平面ABCD，BF＝1.

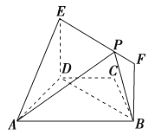
    (1)求证：AD⊥平面BFED；

    (2)点P在线段EF上运动，设平面PAB与平面ADE所成锐二面角为θ，试求θ的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（多选题）下列说法正确的是（ ）

    A.椭圆1上任意一点（非左右顶点）与左右顶点连线的斜率乘积为

    B.过双曲线1焦点的弦中最短弦长为

    C.抛物线y2＝2px上两点A（x1，y1）．B（x2，y2），则弦AB经过抛物线焦点的充要条件为x1x2

    D.若直线与圆锥曲线有一个公共点，则该直线和圆锥曲线相切

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，以为极点，轴为正半轴为极轴建立极坐标系.已知曲线的极坐标方程为 ，直线与曲线相交于两点，直线过定点且倾斜角为交曲线于两点.

    （1）把曲线化成直角坐标方程，并求的值；

    （2）若成等比数列，求直线的倾斜角.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如果你留心使会发现，汽车前灯后的反射镜呈抛物线的形状，把抛物线沿它的对称轴旋转一周，就会形成一个抛物面．这种抛物面形状，正是我们熟悉的汽车前灯的反射镜形状，这种形状使车灯既能够发出明亮的、照射很远的平行光束，又能发出较暗的，照射近距离的光线．我们都知道常规的前照灯主要是由灯泡、反射镜和透镜三部分组成，明亮的光束，是由位于抛物面形状反射镜焦点的光源射出的，灯泡位于抛物面的焦点上，灯泡发出的光经抛物面反射镜反射形成平行光束，再经过配光镜的散射、偏转作用，以达到照亮路面的效果，这样的灯光我们通常称为远光灯：而较暗的光线，不是由反射镜焦点的光源射出的，光线的行进与抛物线的对称轴不平行，光线只能向上和向下照射，所以照射距离并不远，如果把向上射出的光线遮住．车灯就只能发出向下的、射的很近的光线了．请用数学的语言归纳表达远光灯的照明原理，并证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充,已知金字塔的每一条棱和边都相等.

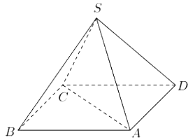
    (1)求证:直线AC垂直于直线SD；

    (2)若搭边框共使用木料24米，则需要多少立方米的填充材料才能将整个金字塔内部填满?

    查看答案和解析>>

    同步练习册答案