
分析 (Ⅰ)根据导数写出f1(x),f2(x)归纳出fn(x);
(Ⅱ)由(Ⅰ)知fn(x)的表达式,要求极值点,就要借助导函数,令导函数为0,解出xn,验证是极值后代入解析式即可求出yn.
(Ⅲ)类比求fn(x)的极小值的过程求出gn(x)的极大值,进而求出最值即可.
解答 解:(Ⅰ)fn(x)=(x+n)ex(n∈N*).…(4分)
(Ⅱ)∵fn′(x)=(x+n+1)ex,
∴当x>-(n+1)时,fn′(x)>0;当x<-(n+1)时,fn′(x)<0.
∴当x=-(n+1)时,fn(x)取得极小值fn[-(n+1)]=-e-(n+1)
,即yn=-e-(n+1)(n∈N*).…(8分)
(Ⅲ)∵gn(x)=-[x+(n+1)]2+(n-3)2
∴a=+(n-3)2,
又b=-e-(n+1),
∴a-b=(n-3)2+e-(n+1),
令h(x)=(x-3)2+e-(x+1)(x≥0),则h'(x)=2(x-3)-e-(x+1).…(10分)
∵h'(x)在[0,+∞)单调递增,∴h'(x)≥h'(0)=-6-e-1,
∵h'(3)=-e-4<0,h'(4)=2-e-5>0,
∴存在x0∈(3,4)使得h'(x0)=0.…(12分)
∵h'(x)在[0,+∞)单调递增,
∴当0≤x<x0时,h'(x0)<0;当x>x0时,h'(x0)>0,
即h(x)在[x0,+∞)单调递增,在[0,x0)单调递减,
∴(h(x))min=h(x0),
又∵h(3)=e-4,h(4)=1+e-5,h(4)>h(3),
∴当n=3时,a-b取得最小值e-4.…(14分)
点评 本题主要考查函数、导数、数列以及合情推理等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、分类与整合思想及有限与无限思想.着重考查学生利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}x±y=0$ | B. | 3x±y=0 | C. | $x±\sqrt{3}y=0$ | D. | x±3y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $-\frac{2}{5}$ | C. | $±\frac{2}{5}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{9}-\frac{y^2}{27}=1$ | B. | $\frac{y^2}{9}-\frac{x^2}{27}=1$ | C. | $\frac{y^2}{27}-\frac{x^2}{9}=1$ | D. | $\frac{x^2}{27}-\frac{y^2}{9}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
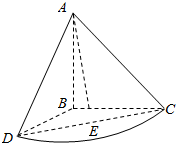 等腰直角三角形ABC中,AB=BC=2,将斜边AC绕直角边AB旋转90°后得到旋转体A-BCD,如图所示,求:
等腰直角三角形ABC中,AB=BC=2,将斜边AC绕直角边AB旋转90°后得到旋转体A-BCD,如图所示,求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com