
【题目】已知函数![]() 在
在![]() 与
与![]() 时都取得极值;
时都取得极值;
(1)求![]() 的值与函数
的值与函数![]() 的单调区间;
的单调区间;
(2)若对![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围
的取值范围
【答案】(1)a=![]() ,b=-2,递增区间是(-,-
,b=-2,递增区间是(-,- ![]() )与(1,+)递减区间是(-
)与(1,+)递减区间是(-![]() ,1)(2)c-1或c2
,1)(2)c-1或c2
【解析】 试题分析:(1)根据极值定义得f(![]() )=0,f(1)=0,解方程组可得
)=0,f(1)=0,解方程组可得![]() 的值,再列表根据导函数符号确定单调区间(2)不等式恒成立问题一般转化为对应函数最值问题:f(x)最大值c2,根据(1)可得f(x)最大值为f(2),解不等式可得
的值,再列表根据导函数符号确定单调区间(2)不等式恒成立问题一般转化为对应函数最值问题:f(x)最大值c2,根据(1)可得f(x)最大值为f(2),解不等式可得![]() 的取值范围
的取值范围
试题解析:解:(1)f(x)=x3+ax2+bx+c,f(x)=3x2+2ax+b
由f(![]() )=
)=![]() ,f(1)=3+2a+b=0得
,f(1)=3+2a+b=0得
a=![]() ,b=-2
,b=-2
f(x)=3x2-x-2=(3x+2)(x-1),函数f(x)的单调区间如下表:
x | (-,- | - | (- | 1 | (1,+) |
f(x) | + | 0 | - | 0 | + |
f(x) | 极大值 | 极小值 |
所以函数f(x)的递增区间是(-,- ![]() )与(1,+)
)与(1,+)
递减区间是(-![]() ,1)
,1)
(2)f(x)=x3-![]() x2-2x+c,x〔-1,2〕,当x=-
x2-2x+c,x〔-1,2〕,当x=-![]() 时,f(x)=
时,f(x)=![]() +c
+c
为极大值,而f(2)=2+c,则f(2)=2+c为最大值。
要使f(x)c2(x〔-1,2〕)恒成立,只需c2f(2)=2+c
解得c-1或c2


科目:高中数学 来源: 题型:
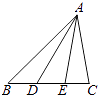
【题目】如图,D、E分别是△ABC的边BC的三等分点,设 ![]() =m,
=m, ![]() =n,∠BAC=
=n,∠BAC= ![]() .
. 
(1)用 ![]() 、
、 ![]() 分别表示
分别表示 ![]() ,
, ![]() ;
;
(2)若 ![]()
![]() =15,|
=15,| ![]() |=3
|=3 ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足a1=1,nan+1=(n+1)an+n(n+1),n∈N* .
(1)证明:数列{ ![]() }是等差数列;
}是等差数列;
(2)设bn=3n ![]() ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以坐标原点![]() 为圆心的圆与抛物线
为圆心的圆与抛物线![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() ,与抛物线
,与抛物线![]() 的准线相交于不同的两点
的准线相交于不同的两点![]() ,
, ![]() ,且
,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若不经过坐标原点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() ,且满足
,且满足![]() .证明直线
.证明直线![]() 过定点
过定点![]() ,并求出点
,并求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义非零向量![]() 的“相伴函数”为
的“相伴函数”为![]() (
(![]() ),向量
),向量![]() 称为函数
称为函数![]() 的“相伴向量”(其中
的“相伴向量”(其中![]() 为坐标原点),记平面内所有向量的“相伴函数”构成的集合为
为坐标原点),记平面内所有向量的“相伴函数”构成的集合为![]() .
.
(1)已知![]() (
(![]() ),求证:
),求证:![]() ,并求函数
,并求函数![]() 的“相伴向量”模的取值范围;
的“相伴向量”模的取值范围;
(2)已知点![]() (
(![]() )满足
)满足![]() ,向量
,向量![]() 的 “相伴函数”
的 “相伴函数”![]() 在
在![]() 处取得最大值,当点
处取得最大值,当点![]() 运动时,求
运动时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位将举办庆典活动,要在广场上竖立一形状为等腰梯形的彩门BADC (如图),设计要求彩门的面积为S (单位:m2)高为h(单位:m)(S,h为常数),彩门的下底BC固定在广场地面上,上底和两腰由不锈钢支架构成,设腰和下底的夹角为α,不锈钢支架的长度和记为l. 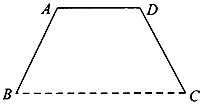
(1)请将l表示成关于α的函数l=f(α);
(2)问当α为何值时l最小?并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京市某年11月1日—20日监测最高最低温度及差值数据如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
最高温度(℃) | 20 | 16 | 14 | 20 | 20 | 20 | 18 | 15 | 12 | 11 | 12 | 12 | 13 | 9 | 8 | 6 | 13 | 11 | 10 | 14 |
最低温度(℃) | 5 | 4 | 2 | 4 | 9 | 6 | 9 | 3 | -1 | 0 | 5 | 1 | 4 | -1 | -4 | -2 | -1 | 0 | 1 | 3 |
差值(℃) | 15 | 12 | 12 | 16 | 11 | 14 | 9 | 12 | 13 | 11 | 7 | 11 | 9 | 10 | 12 | 8 | 14 | 11 | 9 | 11 |
(Ⅰ)完成下面的频率分布表及频率分布直方图,并写出频率分布直方图中![]() 的值;
的值;


(Ⅱ)从日温差大于等于![]() 的这些天中,随机选取2天.求这两天中至少有一天的温差在区间
的这些天中,随机选取2天.求这两天中至少有一天的温差在区间![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com