
【题目】已知函数![]() 是
是![]() 上的奇函数.
上的奇函数.
(1)求实数![]() 的值;
的值;
(2)若![]() ,则不等式
,则不等式![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 且
且![]() 在
在![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由题意得出![]() ,求出
,求出![]() 的值,然后再利用奇函数的定义验证函数
的值,然后再利用奇函数的定义验证函数![]() 为奇函数即可;
为奇函数即可;
(2)由![]() 可得出
可得出![]() ,分析出函数
,分析出函数![]() 在
在![]() 上为增函数,再由
上为增函数,再由![]() 为奇函数,由
为奇函数,由![]() 得出关于
得出关于![]() 的不等式
的不等式![]() 在
在![]() 上有解,可得出
上有解,可得出![]() ,即可求出实数
,即可求出实数![]() 的取值范围;
的取值范围;
(3)由![]() 且
且![]() ,可得出
,可得出![]() ,可得出
,可得出![]() ,换元
,换元![]() ,可得出
,可得出![]() ,然后对
,然后对![]() 分
分![]() 和
和![]() ,分析二次函数
,分析二次函数![]() 在区间
在区间![]() 上的单调性,结合题中条件可求出实数
上的单调性,结合题中条件可求出实数![]() 的值.
的值.
(1)![]() 函数
函数![]() 是
是![]() 上的奇函数,
上的奇函数,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,定义域为
,定义域为![]() ,关于原点对称,
,关于原点对称,
且![]() ,此时函数
,此时函数![]() 为奇函数,因此,
为奇函数,因此,![]() ;
;
(2)由(1)可知![]() ,又
,又![]() ,
,![]() ,解得
,解得![]() .
.
则函数![]() 在
在![]() 上为增函数,函数
上为增函数,函数![]() 在
在![]() 上为减函数,
上为减函数,
![]() 函数
函数![]() 在
在![]() 上是增函数且为奇函数,
上是增函数且为奇函数,
由![]() ,得
,得![]() 在
在![]() 上有解,
上有解,
![]() 在
在![]() 上有解,即
上有解,即![]() 在
在![]() 上有解,
上有解,
![]() ,解得
,解得![]() 或
或![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() ;
;
(3)![]() ,即
,即![]() ,
,![]() 且
且![]() ,解得
,解得![]() .
.
![]() ,令
,令![]() ,又
,又![]() ,则
,则![]() .
.
![]() ,
,![]() .
.
则![]() ,令
,令![]() ,
,
二次函数![]() 图象的对称轴为直线
图象的对称轴为直线![]() .
.
①当![]() 时,函数
时,函数![]() 在
在![]() 为增函数,
为增函数,![]() ,即
,即![]() 不合乎题意;
不合乎题意;
②当![]() 时,
时,![]() 在
在![]() 为增函数,在
为增函数,在![]() 为减函数,
为减函数,
![]() ,
,![]() 满足.
满足.
综上所述,![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知函数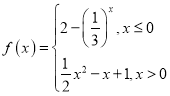 .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)画出该函数的图象,并写出该函数的单调区间(不用证明);
(3)若函数![]() 恰有3个不同零点,求实数
恰有3个不同零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次体能测试中,某研究院对该地区甲、乙两学校做抽样调查,所得学生的测试成绩如下表所示:

(1)将甲、乙两学校学生的成绩整理在所给的茎叶图中,并分别计算其平均数;
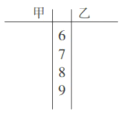
(2)若在乙学校被抽取的10名学生中任选3人检测肺活量,求被抽到的3人中,至少2人成绩超过80分的概率;
(3)以甲学校的体能测试情况估计该地区所有学生的体能情况,则若从该地区随机抽取4名学生,记测试成绩在80分以上(含80分)的人数为![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,若双曲线上存在点
,若双曲线上存在点![]() ,使
,使![]() ,则该双曲线的离心率
,则该双曲线的离心率![]() 范围为( )
范围为( )
A. (1,1![]() ) B. (1,1
) B. (1,1![]() ) C. (1,1
) C. (1,1![]() ] D. (1,1
] D. (1,1![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 的“不动点”;若
的“不动点”;若![]() ,则称
,则称![]() 为
为![]() 的“稳定点”.函数
的“稳定点”.函数![]() 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为![]() 和
和![]() ,即
,即![]() ,
,![]() .
.
(![]() )设函数
)设函数![]() ,求集合
,求集合![]() 和
和![]() .
.
(![]() )求证:
)求证:![]() .
.
(![]() )设函数
)设函数![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下判断正确的是 ( )
A. 函数![]() 为
为![]() 上的可导函数,则
上的可导函数,则![]() 是
是![]() 为函数
为函数![]() 极值点的充要条件
极值点的充要条件
B. 若命题![]() 为假命题,则命题
为假命题,则命题![]() 与命题
与命题![]() 均为假命题
均为假命题
C. 若![]() ,则
,则![]() 的逆命题为真命题
的逆命题为真命题
D. 在![]() 中,“
中,“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com