
【题目】如图所示,ABCDA1B1C1D1是正方体,画出图中阴影部分的平面与平面ABCD的交线,并给出证明.

【答案】见解析
【解析】试题分析:过点E作EN⊥CD于点N,连接NB并延长,交EF的延长线于点M,连接AM,则直线AM为所求。证明时可证明点A,M同时在平面AEF和平面ABCD上即可。
试题解析:

如图,过点E作EN⊥CD于点N,
连接NB并延长,交EF的延长线于点M,连接AM。
则直线AM即为图中阴影部分的平面与平面ABCD的交线。
证明如下:
因为直线EN∥BF,
所以B,N,E,F四点共面,
因此EF与BN相交,交点为M,
因为M∈EF,且M∈NB,
因为EF平面AEF,NB平面ABCD,
所以M是平面ABCD与平面AEF的公共点,
又因为点A是平面AEF和平面ABCD的公共点,
所以AM为这两平面的交线.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】微信是现代生活进行信息交流的重要工具,若要调查某公司使用微信的员工经常使用微信与年龄的关系,并规定每天使用微信时间在一小时以上为经常使用微信。据统计,该公司200名员工中90%的人使用微信,其中不经常使用微信的有60人,其余经常使用微信。若将员工年龄分成青年(年龄小于40岁)和中年(年龄不小于40岁)两个阶段,使用微信的中75%是青年人.经常使用微信的员工中,有80人是青年人.
(1)请完成如下![]() 联列表,
联列表,
青年人 | 中年人 | 合计 | |
经常使用微信 | |||
不经常使用微信 | |||
合计 |
(2)由列联表中所得数据,是否有99.9%的把握认为“经常使用微信与年龄有关”?
(3)现采用分层抽样的方法从“经常使用微信的人”中抽取6人,从已抽取的这6人中任选2人,求“选出的2人均为青年人”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
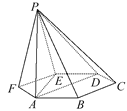
【题目】如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论中:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°.
其中正确的有____________(把所有正确的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中错误的是( )
A. 如果平面![]() 外的直线
外的直线![]() 不平行于平面
不平行于平面![]() ,则平面
,则平面![]() 内不存在与
内不存在与![]() 平行的直线
平行的直线
B. 如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,那么直线
,那么直线![]() 平面
平面![]()
C. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内所有直线都垂直于平面
内所有直线都垂直于平面![]()
D. 一条直线与两个平行平面中的一个平面相交,则必与另一个平面相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(1)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;
(2)现袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“菊花”型烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点时爆裂.通过研究,发现该型烟花爆裂时距地面的高度![]() (单位:米)与时间
(单位:米)与时间![]() (单位:秒)存在函数关系,并得到相关数据如表:
(单位:秒)存在函数关系,并得到相关数据如表:
时间 | 1 |
|
|
高度 |
|
|
|
(1)根据表中数据,从下列函数中选取一个函数描述该型烟花爆裂时距地面的高度![]() 与时间
与时间![]() 的变化关系:
的变化关系: ![]() ,
, ![]() ,
, ![]() ,确定此函数解析式并简单说明理由;
,确定此函数解析式并简单说明理由;
(2)利用你选取的函数,判断烟花爆裂的最佳时刻,并求此时烟花距地面的高度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且
,且![]() 的离心率为
的离心率为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过![]() 的顶点
的顶点![]() 作两条互相垂直的直线与椭圆分别相交于
作两条互相垂直的直线与椭圆分别相交于![]() 两点.若
两点.若![]() 的角平分线方程为
的角平分线方程为![]() ,求
,求![]() 的面积及直线
的面积及直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com