
【题目】已知椭圆C: ![]() 的右焦点为F,不垂直x轴且不过F点的直线l与椭圆C相交于A,B两点.
的右焦点为F,不垂直x轴且不过F点的直线l与椭圆C相交于A,B两点.
(Ⅰ)若直线l经过点P(2,0),则直线FA、FB的斜率之和是否为定值?若是,求出该定值;若不是,请说明理由;
(Ⅱ)如果FA⊥FB,原点到直线l的距离为d,求d的取值范围.
【答案】解:(I)直线l的方程为y=k(x﹣2),
联立方程组 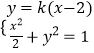 ,消元得(1+2k2)x2﹣8k2x+8k2﹣2=0,
,消元得(1+2k2)x2﹣8k2x+8k2﹣2=0,
设A(x1 , y1),B(x2 , y2),则x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
又F(1,0),∴kFA= ![]() =
= ![]() ,kFB=
,kFB= ![]() =
= ![]() ,
,
∴kFA+kFB= ![]() +
+ ![]() =
= ![]() ,
,
又2kx1x2﹣3k(x1+x2)+4k=2k ![]() ﹣3k
﹣3k ![]() +4k=
+4k= ![]() =0,
=0,
∴kFA+kFB=0,
即直线FA、FB的斜率之和是定值0.
(II)设直线l的方程为y=kx+b,
联立方程组 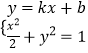 ,消去y得(1+2k2)x2+4kbx+2(b2﹣1)=0,
,消去y得(1+2k2)x2+4kbx+2(b2﹣1)=0,
∴△=16k2b2﹣8(1+2k2)(b2﹣1)=8(2k2+1﹣b2)>0,
设A(x3 , y3),B(x4 , y4),则x3+x4= ![]() ,x3x4=
,x3x4= ![]() ,
,
∴kFA= ![]() =
= ![]() ,kFB=
,kFB= ![]() =
= ![]() ,
,
若FA⊥FB,则 ![]()
![]() =﹣1,
=﹣1,
即(k2+1)x3x4+(kb﹣1)(x3+x4)+b2+1=0,
∴(k2+1) ![]() +(kb﹣1)
+(kb﹣1) ![]() +b2+1=0,
+b2+1=0,
化简得3b2+4kb﹣1=0,即k= ![]() ,
,
代入判别式得△=b4+2b2+1>0恒成立,
∴d= ![]() =
= 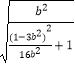 =
= 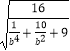 ,
,
∵ ![]() +
+ ![]() +9>9,
+9>9,
∴d< ![]() =
= ![]() .
.
∴d的取值范围是(0,9)
【解析】(I)联立方程组,根据根与系数的关系得出A,B两点坐标的关系,表示出直线AF,BF的斜率,计算斜率之和作出判断;(II)设直线l的方程为y=kx+b,联立方程组,根据根与系数的关系得出A,B两点坐标的关系,表示出直线AF,BF的斜率,令斜率之积为﹣1得出k,b的关系,代入距离公式得出d与b的关系,根据判别式得出b的范围,从而得出d的范围.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知三棱锥 ![]() ,底面
,底面 ![]() 是以
是以 ![]() 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形, ![]() ,
, ![]() ,二面角
,二面角 ![]() 的大小为
的大小为 ![]() .
.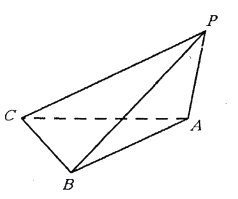
(1)求直线 ![]() 与平面
与平面 ![]() 所成角的大小;
所成角的大小;
(2)求二面角 ![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高一年级期中考试的学生中随机抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,观察图形的信息,回答下列问题:
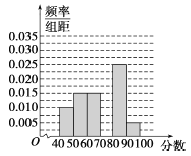
(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试中的平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少.把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元.现在这种羊毛衫的成本价是100元/ 件,商场以高于成本价的价格(标价)出售. 问:
(1)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(2)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,过对角线
中,过对角线![]() 的一个平面交
的一个平面交![]() 于点
于点![]() ,交
,交![]() 于
于![]() .
.
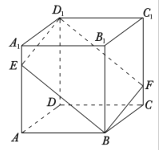
①四边形![]() 一定是平行四边形;
一定是平行四边形;
②四边形![]() 有可能是正方形;
有可能是正方形;
③四边形![]() 在底面
在底面![]() 内的投影一定是正方形;
内的投影一定是正方形;
④四边形![]() 有可能垂直于平面
有可能垂直于平面![]() .
.
以上结论正确的为_______________.(写出所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 ![]() (t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2.
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2.
(Ⅰ)证明:不论t为何值,直线l与曲线C恒有两个公共点;
(Ⅱ)以α为参数,求直线l与曲线C相交所得弦AB的中点轨迹的参数方程,并判断该轨迹的曲线类型.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|+|x﹣1|,a∈R.
(Ⅰ)若不等式f(x)≥2﹣|x﹣1|恒成立,求实数a的取值范围;
(Ⅱ)当a=1时,直线y=m与函数f(x)的图象围成三角形,求m的最大值及此时围成的三角形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下关于命题的说法正确的有(填写所有正确命题的序号).
①“若 ![]() ,则函数
,则函数 ![]() (
( ![]() ,且
,且 ![]() )在其定义域内是减函数”是真命题;
)在其定义域内是减函数”是真命题;
②命题“若 ![]() ,则
,则 ![]() ”的否命题是“若
”的否命题是“若 ![]() ,则
,则 ![]() ”;
”;
③命题“若 ![]() ,
, ![]() 都是偶数,则
都是偶数,则 ![]() 也是偶数”的逆命题为真命题;
也是偶数”的逆命题为真命题;
④命题“若 ![]() ,则
,则 ![]() ”与命题“若
”与命题“若 ![]() ,则
,则 ![]() ”等价.
”等价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com