
【题目】德国数学家科拉茨1937年提出一个著名的猜想:任给一个正整数![]() ,如果
,如果![]() 是偶数,就将它减半(即
是偶数,就将它减半(即![]() );如果
);如果![]() 是奇数,则将它乘3加1(即
是奇数,则将它乘3加1(即![]() ),不断重复这样的运算,经过有限步后,一定可以得到1.对于科拉茨猜想,目前谁也不能证明,也不能否定.现在请你研究:如果对正整数
),不断重复这样的运算,经过有限步后,一定可以得到1.对于科拉茨猜想,目前谁也不能证明,也不能否定.现在请你研究:如果对正整数![]() (首项)按照上述规则进行变换后的第9项为1(注:1可以多次出现),则
(首项)按照上述规则进行变换后的第9项为1(注:1可以多次出现),则![]() 的所有不同值的个数为( )
的所有不同值的个数为( )
A. 4 B. 5 C. 6 D. 7
科目:高中数学 来源: 题型:
【题目】设函数![]()
![]() .若曲线
.若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的单调区间;
的单调区间;
(2)若关于![]() 的不等式
的不等式![]() 在(0,+
在(0,+![]() )上恒成立,求实数
)上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系![]() 中,平行于
中,平行于![]() 轴且过点
轴且过点![]() 的入射光线
的入射光线![]() 被直线
被直线![]() 反射,反射光线
反射,反射光线![]() 交
交![]() 轴于
轴于![]() 点,圆
点,圆![]() 过点
过点![]() ,且与
,且与![]() 、
、![]() 相切.
相切.
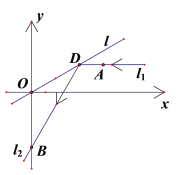
(Ⅰ)求![]() 所在直线的方程;
所在直线的方程;
(Ⅱ)求圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以平面直角坐标系
为参数),以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 上的动点
上的动点![]() 到坐标原点
到坐标原点![]() 的距离
的距离![]() 的最大值;
的最大值;
(Ⅱ)若曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且与
两点,且与![]() 轴相交于点
轴相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)函数![]() 与函数
与函数![]() 的图像总有两个交点,设这两个交点的横坐标分别为
的图像总有两个交点,设这两个交点的横坐标分别为![]() ,
,![]() .
.
(ⅰ)求![]() 的取值范围;
的取值范围;
(ⅱ)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射击运动员进行射击训练,前三次射击在靶上的着弹点![]() 刚好是边长为
刚好是边长为![]() 的等边三角形的三个顶点.
的等边三角形的三个顶点.

(Ⅰ)第四次射击时,该运动员瞄准![]() 区域射击(不会打到
区域射击(不会打到![]() 外),则此次射击的着弹点距
外),则此次射击的着弹点距![]() 的距离都超过
的距离都超过![]() 的概率为多少?(弹孔大小忽略不计)
的概率为多少?(弹孔大小忽略不计)
(Ⅱ) 该运动员前三次射击的成绩(环数)都在区间![]() 内,调整一下后,又连打三枪,其成绩(环数)都在区间
内,调整一下后,又连打三枪,其成绩(环数)都在区间![]() 内.现从这
内.现从这![]() 次射击成绩中随机抽取两次射击的成绩(记为
次射击成绩中随机抽取两次射击的成绩(记为![]() 和
和![]() )进行技术分析.求事件“
)进行技术分析.求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com