
【题目】已知函数![]() .
.
(Ⅰ)若函数f(x)的最小值为8,求实数a的值;
(Ⅱ)若函数g(x)=|f(x)|+f(x)﹣16有4个零点,求实数a的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)利用换元法,结合二次函数进行分类讨论求解;
(Ⅱ)先求![]() 的零点,结合二次方程根的分布情况可得实数a的取值范围.
的零点,结合二次方程根的分布情况可得实数a的取值范围.
(Ⅰ)函数![]() ,
,
令![]() ,易知t∈(﹣∞,﹣2]∪[2,+∞),则h(t)=t2﹣2at+2a2﹣2在(﹣∞,﹣2]∪[2,+∞)上的最小值为8,函数h(t)的对称轴为t=a,
,易知t∈(﹣∞,﹣2]∪[2,+∞),则h(t)=t2﹣2at+2a2﹣2在(﹣∞,﹣2]∪[2,+∞)上的最小值为8,函数h(t)的对称轴为t=a,
①当a≥2时,![]() ,此时
,此时![]() ;
;
②当a≤﹣2时,![]() ,此时
,此时![]() ;
;
③当﹣2<a<0时,![]() ,此时无解;
,此时无解;
④当0≤a<2时,![]() =h(2)=2a2﹣4a+2=8,此时无解;
=h(2)=2a2﹣4a+2=8,此时无解;
故实数a的值为![]() .
.
(Ⅱ)令g(x)=0,则f(x)=8,
则由题意,方程t2﹣2at+2a2﹣2=8,即t2﹣2at+2a2﹣10=0必有两根,且一根小于﹣2,另一根大于2,
则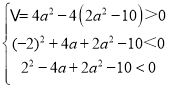 ,解得﹣1<a<1.
,解得﹣1<a<1.
故实数a的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】当前全世界人民越来越关注环境保护问题,某地某监测站点于2018年8月起连续n天监测空气质量指数(AQI),数据统计如下表:
空气质量指数(μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] |
空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 20 | 40 | m | 10 | 5 |
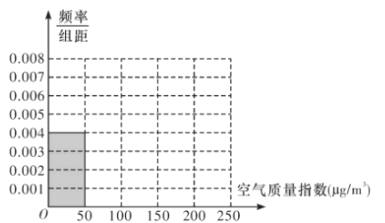
(1)根据所给统计表和频率分布直方图中的信息求出n,m的值,并完成频率分布直方图;
(2)由频率分布直方图,求该组数据的平均数与中位数;
(3)在空气质量指数分别为[0,50]和(50,100]的监测数据中,用分层抽样的方法抽取6天,从中任意选取2天,求事件A“两天空气质量等级都为良”发生的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬果经销商销售某种蔬果,售价为每公斤25元,成本为每公斤15元.销售宗旨是当天进货当天销售.如果当天卖不出去,未售出的全部降价以每公斤10元处理完.根据以往的销售情况,得到如图所示的频率分布直方图:

(1)根据频率分布直方图计算该种蔬果日需求量的平均数![]() (同一组中的数据用该组区间中点值代表);
(同一组中的数据用该组区间中点值代表);
(2)该经销商某天购进了250公斤这种蔬果,假设当天的需求量为![]() 公斤
公斤![]() ,利润为
,利润为![]() 元.求
元.求![]() 关于
关于![]() 的函数关系式,并结合频率分布直方图估计利润
的函数关系式,并结合频率分布直方图估计利润![]() 不小于1750元的概率.
不小于1750元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济全球化、信息化的发展,企业之间的竞争从资源的争夺转向人才的竞争.吸引、留住培养和用好人才成为人力资源管理的战略目标和紧迫任务.在此背景下,某信息网站在15个城市中对刚毕业的大学生的月平均收入薪资和月平均期望薪资做了调查,数据如图所示.
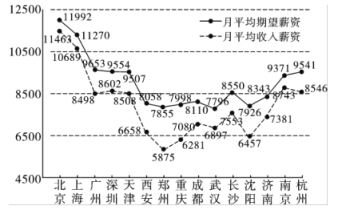
(1)若某大学毕业生从这15座城市中随机选择一座城市就业,求该生选中月平均收人薪资高于8000元的城市的概率;
(2)若从月平均收入薪资与月平均期望薪资之差高于1000元的城市中随机选择2座城市,求这2座城市的月平均期望薪资都高于8000元或都低于8000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面四边形![]() 中,
中,![]() ,
,![]() 是
是![]() ,
,![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起至
折起至![]() ,使平面
,使平面![]() ,则四面体
,则四面体![]() 中,下列结论不正确的是( )
中,下列结论不正确的是( )
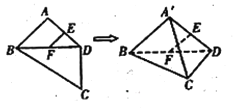
A.![]() 平面
平面![]()
B.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
C.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
D.直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com