
����Ŀ��ij��ѧ�Ը���ѧ���������ܲ��ԣ���֪����ij�Ŀư���ѧ��30�ˣ�������Զ�IJ��Գɼ��þ�Ҷͼ��ʾ��ͼ(��λ: ![]() )�������ɼ���
)�������ɼ���![]() ����(����
����(����![]() )����Ϊ���ϸ��ɼ���
)����Ϊ���ϸ��ɼ���![]() ����(������
����(������![]() )����Ϊ�����ϸ�Ů���ɼ���
)����Ϊ�����ϸ�Ů���ɼ���![]() ����(����
����(����![]() )����Ϊ���ϸ��ɼ���
)����Ϊ���ϸ��ɼ���![]() ����(������
����(������![]() )����Ϊ�����ϸ�.
)����Ϊ�����ϸ�.
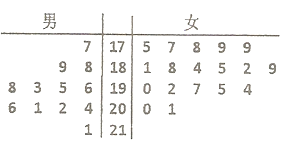
��1����Ů��������Զ���Գɼ�����λ����
��2�����������а��ɼ��Ƿ�ϸ���зֲ��������ȡ6�ˣ����ȡ�ɼ�Ϊ���ϸ�ѧ��������
��3�����ӣ�2���г�ȡ��6������������ѡȡ4�ˣ�����4����������3�ˡ��ϸĸ���.
���𰸡���1��![]()
![]() ����2��4�ˣ���3��
����2��4�ˣ���3��![]() .
.
�������������������1���ɾ�Ҷͼ�����Ů��������Զ�ɼ�����λ������2�������ɼ����ϸ���8�ˣ������ϸ���4�ˣ��÷ֲ�����ķ�������������гɼ����ϸ�ѧ��Ӧ��ȡ����������3���ɣ�2����֪6���У�4�˺ϸ�2�˲��ϸ���ϸ�ѧ��Ϊ a��b��c��d ���ϸ�ѧ��Ϊe��f�������оٷ��������4��������3�˺ϸ�ĸ��ʣ�
���������
��1��Ů��������Զ�ɼ�����λ��Ϊ�� ![]()
![]()
��2�������ɼ����ϸ�8�ˣ������ϸ���4�ˣ��÷ֲ�����ķ�������ȡ�ɼ�Ϊ���ϸ�ѧ������![]() ���ˣ�
���ˣ�
��3���ɣ�2��֪6���У�4�˺ϸ�2�˲��ϸ�
��ϸ�ѧ��Ϊ![]() �����ϸ�ѧ��
�����ϸ�ѧ��![]() ��
��
��6������ȡ4�ˣ���![]() ��15�������¼�.
��15�������¼�.
���з�����������9�ˣ���![]() .
.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��
��1����������[0��1]�������ֵ1����Сֵ-2����a��b��ֵ��
��2���ڣ�1�������£���������![]() �ϣ�����ʽf��x��
�ϣ�����ʽf��x��![]()
![]() ���������ʵ��m��ȡֵ��Χ��
���������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ��
��![]() ��
��![]() �����溯����
�����溯����
��1������![]() ��ֵ��
��ֵ��
��2����![]() �����жϺ���
�����жϺ���![]() �ĵ����ԣ�������֤����
�ĵ����ԣ�������֤����
��3����![]() ���Һ���
���Һ���![]() ������
������![]() �ϵ���СֵΪ
�ϵ���СֵΪ![]() ����ʵ��
����ʵ��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪Բ
�У���֪Բ![]() ����
����![]() ��
�� ![]() ���㣬��Բ����ֱ��
���㣬��Բ����ֱ��![]() �ϣ�
�ϣ�
��1����Բ![]() �ı����̣�
�ı����̣�
��2����Բ![]() ��һ��
��һ��![]() ���������ֱ����
���������ֱ����![]() ����
����![]() ʱ�����ı���
ʱ�����ı���![]() �������
�������
��3����ֱ��![]() ��Բ
��Բ![]() �ཻ��
�ཻ��![]() ���㣬
���㣬 ![]() ����
����![]() �����Ϊ
�����Ϊ![]() ����ֱ��
����ֱ��![]() �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCA1B1C1�У�AB��2��AA1��3��
DΪC1B���е㣬PΪAB���ϵĶ���.
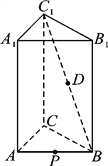
(1)����PΪAB���е�ʱ��֤��DP��ƽ��ACC1A1��
(2)��AP��3PB��������BCDP�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ú졢�ơ���������ɫ����ͼ��ʾ������������ԲͿɫ����ÿ����ɫֻ��Ϳ����Բ������������Բ��Ϳ��ɫ������ͬ����ͬ��Ϳɫ�����������ǣ� �� ![]()
A.12
B.24
C.30
D.36
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����Ϊ�˽����¶�Ӫҵ���Ӱ�죬�����¼�˸õ�1�·���5�����Ӫҵ��y����λ��ǧԪ����õص����������x����λ���棩�����ݣ������
x | 2 | 8 | 9 | 11 | 5 |
y | 12 | 8 | 8 | 7 | 10 |
��1����y����x�Ļع鷽�� ![]() ��
��
��2���ж�y��x֮��������ػ��Ǹ���أ����õ�1�·�ij����������Ϊ6�棬������ع鷽��Ԥ��õ굱�յ�Ӫҵ� �������ع鷽�� ![]() �У�
�У� ![]() =
= 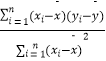 =
=  ��
�� ![]() =
= ![]() ��
�� ![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l����ֱ��2x��y��5��0��x��2y��0�Ľ���P.
(1)��A(5��0)��ֱ��l�ľ���Ϊ3����ֱ��l�ķ��̣�
(2)���A(5��0)��ֱ��l�ľ�������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������20����С��ͬ�������м���0�ŵ���10��������n�ŵ���n����n��1,2,3,4�����ִӴ�����ȡһ��X��ʾ��ȡ��ı��.
��1����X�ķֲ��У���ֵ�ͷ��
��2����Y��aX��b��E��Y����1��D��Y����11������a��b��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com