Question

【题目】从某校高三年级800名学生中随机抽取50名测量身高，据测量被抽取的学生的身高全部介于155cm和195cm之间，将测量结果按如下方式分成八组：第一组[155,160)，第二组[160,165)，……，第八组[190.195]，下图是按上述分组方法得到的频率分布直方图．

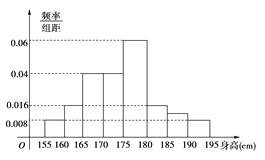
（1）求第七组的频数；

(2)试估计这所学校高三年级800名学生中身高在180cm以上(含180cm)的人数为多少.

Answer 1

【答案】(1) 3. (2) 144.

【解析】

试题(1)由频率分布直方图得第七组频率为：1－(0.008×2＋0.016×2＋0.04×2＋0.06)×5＝0.06，

∴第七组的人数为0.06×50＝3.

由各组频率可得以下数据：

组别	一	二	三	四	五	六	七	八
样本数	2	4	10	10	15	4	3	2

(2)由频率分布直方图得后三组频率和为0.08＋0.06＋0.04＝0.18，

估计这所学校高三年级800名学生中身高在180cm以上(含180cm)的人数为800×0.18＝144.