
【题目】已知函数f(x)=3x+λ3﹣x(λ∈R).
(1)当λ=﹣4时,求函数f(x)的零点;
(2)若函数f(x)为偶函数,求实数λ的值;
(3)若不等式f(x)≤6在x∈[0,2]上恒成立,求实数λ的取值范围.
【答案】解:(1)当λ=﹣4时,f(x)=3x﹣43﹣x ,
令f(x)=0,得3x﹣43﹣x=0,
即(3x)2﹣4=0,解得x=log32.
故函数f(x)的零点为log32;
(2)∵f(x)为偶函数,∴f(﹣x)=f(x).
∴3﹣x+λ3x=3x+λ3﹣x , 即(1﹣λ)(3﹣x﹣3x)=0.
又∵3﹣x﹣3x不恒为零,
∴1﹣λ=0,即λ=1;
(3)由f(x)≤6,得3x+λ3﹣x≤6,
即![]() .
.
令t=3x∈[1,9],原不等式等价于t+![]() 在t∈[1,9]恒成立.
在t∈[1,9]恒成立.
亦即λ≤﹣t2+6t在t∈[1,9]上恒成立.
令g(t)=﹣t2+6t,t∈[1,9].
当t=9时,g(t)有最小值g(9)=﹣27.
∴λ≤﹣27.
【解析】(1)把λ=﹣4代入函数解析式,求解指数方程求得函数f(x)的零点;
(2)直接利用偶函数的性质列式求得λ的值;
(3)由不等式f(x)≤6在x∈[0,2]上恒成立,分离参数λ,换元后利用配方法求得最小值得答案.
【考点精析】认真审题,首先需要了解函数奇偶性的性质(在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇).


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() 的定义域为A,集合B={x|(x﹣m﹣3)(x﹣m+3)≤0}.
的定义域为A,集合B={x|(x﹣m﹣3)(x﹣m+3)≤0}.
(1)求A和f(x)的值域C;
(2)若A∩B=[2,3],求实数m的值;
(3)若CRB,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司制定了一个激励销售人员的奖励方案:当销售利润不超过20万元时,按销售利润的20%进行奖励;当销售利润超过20万元时,若超出部分为A万元,则超出部分按2log5(A+2)进行奖励,没超出部分仍按销售利润的20%进行奖励.记奖金总额为y(单位:万元),销售利润为x(单位:万元).
(1)写出该公司激励销售人员奖励方案的函数表达式;
(2)如果业务员老张获得8万元的奖励,那么他的销售利润是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=![]() (弦×矢+矢2).弧田,由圆弧和其所对弦所围成.公式中“弦”指圆弧对弦长,“矢”等于半径长与圆心到弦的距离之差,按照上述经验公式计算所得弧田面积与实际面积之间存在误差.现有圆心角为
(弦×矢+矢2).弧田,由圆弧和其所对弦所围成.公式中“弦”指圆弧对弦长,“矢”等于半径长与圆心到弦的距离之差,按照上述经验公式计算所得弧田面积与实际面积之间存在误差.现有圆心角为![]() π,弦长等于9米的弧田.按照《九章算术》中弧田面积的经验公式计算所得弧田面积与实际面积的差为
π,弦长等于9米的弧田.按照《九章算术》中弧田面积的经验公式计算所得弧田面积与实际面积的差为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车的出现方便了人们的出行,深受市民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)频率分布直方图.
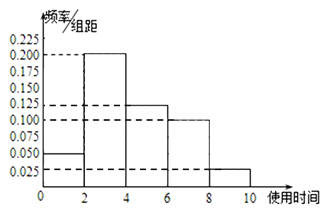
(1)已知该校大一学生有2400人,求抽取的100名学生中大一学生人数;
(2)根据频率分布直方图求该校大学生每周使用共享单车的平均时间.
(3)![]() 从抽取的100个样本中,用分层抽样的方法抽取使用共享单车时间超过6小时同学5人,再从这5人中任选2人,求这2人使用共享单车时间都不超过8小时的概率.
从抽取的100个样本中,用分层抽样的方法抽取使用共享单车时间超过6小时同学5人,再从这5人中任选2人,求这2人使用共享单车时间都不超过8小时的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=kx(k≠0),且满足f(x+1)f(x)=x2+x,
(1)求函数f(x)的解析式;
(2)若函数f(x)为R上的增函数,h(x)= ![]() (f(x)≠1),问是否存在实数m使得h(x)的定义域和值域都为[m,m+1]?若存在,求出m的值,若不存在,请说明理由.
(f(x)≠1),问是否存在实数m使得h(x)的定义域和值域都为[m,m+1]?若存在,求出m的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com