已知命题:
①已知正项等比数列{an}中,不等式an+1+an-1≥2an(n≥2,n∈N*)一定成立;
②若F(n)=(n+1)(n+2)(n+3)…(n+n)(n∈N*),则F(1)=2,F(2)=24;
③已知数列{an}中,an=n2+λn+1(λ∈R).若λ>-3,则恒有an+1>an(n∈N*);
④公差小于零的等差数列{an}的前n项和为Sn.若S20=S40,则S30为数列{Sn}的最大项;以上四个命题正确的是 (填入相应序号)
【答案】
分析:由正项等比数列{a
n}中,a
n+1,a
n,a
n-1(n≥2,n∈N
*)成等差数列,知a
n+1+a
n-1=2a
n(n≥2,n∈N
*);由F(n)=(n+1)(n+2)(n+3)…(n+n)(n∈N
*),知F(1)=1+1=2,F(2)=(2+1)(2+2)=12≠24;由λ>-3知a
n+1-a
n=[(n+1)
2+λ(n+1)+1]-(n
2+λn+1)=2n+1+λ>0;由公差小于零的等差数列{a
n}的前n项和为S
n.S
20=S
40,知20
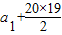
d=40
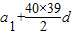
,
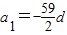
,所以
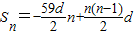
=
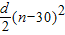
-450d,由d<0,知S
30为数列{S
n}的最大项.
解答:解:∵正项等比数列{a
n}中,a
n+1,a
n,a
n-1(n≥2,n∈N
*)成等差数列,
∴a
n+1+a
n-1=2a
n(n≥2,n∈N
*),
∴不等式a
n+1+a
n-1≥2a
n(n≥2,n∈N
*)一定成立.
故①正确;
∵F(n)=(n+1)(n+2)(n+3)…(n+n)(n∈N
*),
∴F(1)=1+1=2,
F(2)=(2+1)(2+2)=12≠24,
故②不正确;
∵λ>-3
∴a
n+1-a
n=[(n+1)
2+λ(n+1)+1]-(n
2+λn+1)=2n+1+λ>0,
∴若λ>-3,则恒有a
n+1>a
n(n∈N
*),
故③正确;
公差小于零的等差数列{a
n}的前n项和为S
n.
若S
20=S
40,
则20

d=40
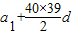
,
∴
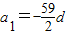
,
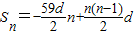
=
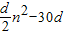
=

-450d,
∵d<0,
∴S
30为数列{S
n}的最大项.
故④正确.
故答案为:①③④.
点评:本题考查数列的性质的应用,是基础题.解题时要认真审题,熟练掌握等差数列和等比数列的性质.

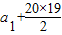 d=40
d=40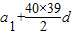 ,
,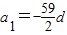 ,所以
,所以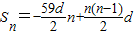 =
=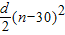 -450d,由d<0,知S30为数列{Sn}的最大项.
-450d,由d<0,知S30为数列{Sn}的最大项. d=40
d=40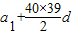 ,
,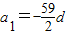 ,
,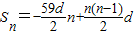
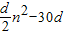
 -450d,
-450d,
