
ЁОЬтФПЁПФГЛљЕиЪпВЫДѓХяВЩгУЫЎХрЁЂЮоЭСддХрЗНЪНжжжВИїРрЪпВЫЃЎЙ§ШЅ50жмЕФзЪСЯЯдЪОЃЌИУЕижмЙтееСП![]() ЃЈаЁЪБЃЉЖМдк30аЁЪБвдЩЯЃЌЦфжаВЛзу50аЁЪБЕФжмЪ§га5жмЃЌВЛЕЭгк50аЁЪБЧвВЛГЌЙ§70аЁЪБЕФжмЪ§га35жмЃЌГЌЙ§70аЁЪБЕФжмЪ§га10жмЃЎИљОнЭГМЦЃЌИУЛљЕиЕФЮїКьЪСдіМгСП
ЃЈаЁЪБЃЉЖМдк30аЁЪБвдЩЯЃЌЦфжаВЛзу50аЁЪБЕФжмЪ§га5жмЃЌВЛЕЭгк50аЁЪБЧвВЛГЌЙ§70аЁЪБЕФжмЪ§га35жмЃЌГЌЙ§70аЁЪБЕФжмЪ§га10жмЃЎИљОнЭГМЦЃЌИУЛљЕиЕФЮїКьЪСдіМгСП![]() ЃЈАйНяЃЉгыЪЙгУФГжжвКЬхЗЪСЯ
ЃЈАйНяЃЉгыЪЙгУФГжжвКЬхЗЪСЯ![]() ЃЈЧЇПЫЃЉжЎМфЖдгІЪ§ОнЮЊШчЭМЫљЪОЕФелЯпЭМЃЎ
ЃЈЧЇПЫЃЉжЎМфЖдгІЪ§ОнЮЊШчЭМЫљЪОЕФелЯпЭМЃЎ

ЃЈ1ЃЉвРОнЪ§ОнЕФелЯпЭМЃЌЪЧЗёПЩгУЯпадЛиЙщФЃаЭФтКЯ![]() гы
гы![]() ЕФЙиЯЕЃПЧыМЦЫуЯрЙиЯЕЪ§
ЕФЙиЯЕЃПЧыМЦЫуЯрЙиЯЕЪ§![]() ВЂМгвдЫЕУїЃЈОЋШЗЕН0.01ЃЉЃЛЃЈШє
ВЂМгвдЫЕУїЃЈОЋШЗЕН0.01ЃЉЃЛЃЈШє![]() ЃЌдђЯпадЯрЙиГЬЖШКмИпЃЌПЩгУЯпадЛиЙщФЃаЭФтКЯЃЉ
ЃЌдђЯпадЯрЙиГЬЖШКмИпЃЌПЩгУЯпадЛиЙщФЃаЭФтКЯЃЉ
ЃЈ2ЃЉЪпВЫДѓХяЖдЙтеевЊЧѓНЯДѓЃЌФГЙтееПижЦвЧЩЬМвЮЊИУЛљЕиЬсЙЉСЫВПЗжЙтееПижЦвЧЃЌЕЋУПжмЙтееПижЦвЧзюЖрПЩдЫааЬЈЪ§ЪмжмЙтееСП![]() ЯожЦЃЌВЂгаШчБэЙиЯЕЃК
ЯожЦЃЌВЂгаШчБэЙиЯЕЃК

ШєФГЬЈЙтееПижЦвЧдЫааЃЌдђИУЬЈЙтееПижЦвЧжмРћШѓЮЊ3000дЊЃЛШєФГЬЈЙтееПижЦвЧЮДдЫааЃЌдђИУЬЈЙтееПижЦвЧжмПїЫ№1000дЊЃЎвдЙ§ШЅ50жмЕФжмЙтееСПЕФЦЕТЪзїЮЊжмЙтееСПЗЂЩњЕФИХТЪЃЌЩЬМвгћЪЙжмзмРћШѓЕФОљжЕДяЕНзюДѓЃЌгІАВзАЙтееПижЦвЧЖрЩйЬЈЃП
ИНЃКЯрЙиЯЕЪ§ЙЋЪН ЃЌВЮПМЪ§Он
ЃЌВЮПМЪ§Он![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЁОД№АИЁП(1)МћНтЮі;(2)ЮЊЪЙЩЬМвжмРћШѓЕФОљжЕДяЕНзюДѓгІИУАВзА2ЬЈЙтееПижЦвЧЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃК(1)гЩелЯпЭМЃЌПЩЕУ![]() ЃЌвРДЮЫуЕУ
ЃЌвРДЮЫуЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌПЩЧѓЕУr
ЃЌПЩЧѓЕУr![]() , ЫљвдПЩгУЯпадЛиЙщФЃаЭФтКЯ
, ЫљвдПЩгУЯпадЛиЙщФЃаЭФтКЯ![]() гы
гы![]() ЕФЙиЯЕ.(2)ЗжБ№МЦЫуАВзА1ЬЈЃЌ2ЬЈЪБЫљЛёжмРћШѓжЕЃЈЦкЭћжЕЃЉЃЌЪ§жЕДѓЕФЮЊЫљбЁдёЁЃ
ЕФЙиЯЕ.(2)ЗжБ№МЦЫуАВзА1ЬЈЃЌ2ЬЈЪБЫљЛёжмРћШѓжЕЃЈЦкЭћжЕЃЉЃЌЪ§жЕДѓЕФЮЊЫљбЁдёЁЃ
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩвбжЊЪ§ОнПЩЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
вђЮЊ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
ЫљвдЯрЙиЯЕЪ§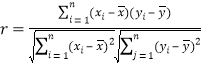
![]() ЃЌ
ЃЌ
вђЮЊ![]() ЃЌЫљвдПЩгУЯпадЛиЙщФЃаЭФтКЯ
ЃЌЫљвдПЩгУЯпадЛиЙщФЃаЭФтКЯ![]() гы
гы![]() ЕФЙиЯЕЃЎ
ЕФЙиЯЕЃЎ
ЃЈ2ЃЉМЧЩЬМвжмзмРћШѓЮЊ![]() дЊЃЌгЩЬѕМўПЩжЊжСЩйашвЊАВзА1ЬЈЃЌзюЖрАВзА3ЬЈЙтееПижЦвЧЃЎ
дЊЃЌгЩЬѕМўПЩжЊжСЩйашвЊАВзА1ЬЈЃЌзюЖрАВзА3ЬЈЙтееПижЦвЧЃЎ
ЂйАВзА1ЬЈЙтееПижЦвЧПЩЛёЕУжмзмРћШѓ3000дЊЃЛ
ЂкАВзА2ЬЈЙтееПижЦвЧЕФЧщаЮЃК
ЕБ![]() ЪБЃЌжЛга1ЬЈЙтееПижЦвЧдЫааЃЌДЫЪБжмзмРћШѓ
ЪБЃЌжЛга1ЬЈЙтееПижЦвЧдЫааЃЌДЫЪБжмзмРћШѓ![]() дЊЃЌ
дЊЃЌ
ЕБ![]() ЪБЃЌ2ЬЈЙтееПижЦвЧЖМдЫааЃЌДЫЪБжмзмРћШѓ
ЪБЃЌ2ЬЈЙтееПижЦвЧЖМдЫааЃЌДЫЪБжмзмРћШѓ![]() дЊЃЌ
дЊЃЌ
ЙЪ![]() ЕФЗжВМСаЮЊЃК
ЕФЗжВМСаЮЊЃК
| 2000 | 6000 |
| 0.2 | 0.8 |
Ыљвд![]() дЊЃЎ
дЊЃЎ
злЩЯПЩжЊЃЌЮЊЪЙЩЬМвжмРћШѓЕФОљжЕДяЕНзюДѓгІИУАВзА2ЬЈЙтееПижЦвЧЃЎ


 ЕМбЇШЋГЬСЗДДгХбЕСЗЯЕСаД№АИ
ЕМбЇШЋГЬСЗДДгХбЕСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() Чв
Чв![]() ЃЉ.
ЃЉ.
ЃЈ1ЃЉЧѓ![]() ЕФЖЈвхгђЃЛ
ЕФЖЈвхгђЃЛ
ЃЈ2ЃЉЬжТлКЏЪ§![]() ЕФЕЅЕїад.
ЕФЕЅЕїад.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮоЧюЪ§Са![]()
![]() ЃЌШєДцдке§ећЪ§
ЃЌШєДцдке§ећЪ§![]() ЃЌЪЙЕУИУЪ§СагЩ
ЃЌЪЙЕУИУЪ§СагЩ![]() ИіЛЅВЛЯрЭЌЕФЪЕЪ§зщГЩЃЌЧвЖдгкШЮвтЕФе§ећЪ§
ИіЛЅВЛЯрЭЌЕФЪЕЪ§зщГЩЃЌЧвЖдгкШЮвтЕФе§ећЪ§![]() ЃЌ
ЃЌ![]() жажСЩйгавЛИіЕШгк
жажСЩйгавЛИіЕШгк![]() ЃЌдђГЦЪ§Са
ЃЌдђГЦЪ§Са![]() ОпгааджЪ
ОпгааджЪ![]() .МЏКЯ
.МЏКЯ![]() .
.
ЃЈ1ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌХаЖЯЪ§Са
ЃЌХаЖЯЪ§Са![]() ЪЧЗёОпгааджЪ
ЪЧЗёОпгааджЪ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЪ§Са![]() ОпгааджЪ
ОпгааджЪ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉЪ§Са![]() ОпгааджЪ
ОпгааджЪ![]() ЃЌЖдгк
ЃЌЖдгк![]() жаЕФШЮвтдЊЫи
жаЕФШЮвтдЊЫи![]() ЃЌ
ЃЌ![]() ЮЊЕк
ЮЊЕк![]() ИіТњзу
ИіТњзу![]() ЕФЯюЃЌМЧ
ЕФЯюЃЌМЧ![]()
![]() ЃЌжЄУїЃКЁАЪ§Са
ЃЌжЄУїЃКЁАЪ§Са![]() ОпгааджЪ
ОпгааджЪ![]() ЁБЕФГфвЊЬѕМўЮЊЁАЪ§Са
ЁБЕФГфвЊЬѕМўЮЊЁАЪ§Са![]() ЪЧжмЦкЮЊ
ЪЧжмЦкЮЊ![]() ЕФжмЦкЪ§СаЃЌЧвУПИіжмЦкОљАќКЌ
ЕФжмЦкЪ§СаЃЌЧвУПИіжмЦкОљАќКЌ![]() ИіВЛЭЌЪЕЪ§ЁБ.
ИіВЛЭЌЪЕЪ§ЁБ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃ![]() УћбЇЩњЕФЪ§бЇЦкжаПМЪдГЩМЈЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪО,ЦфжаГЩМЈЗжзщЧјМфЪЧ
УћбЇЩњЕФЪ§бЇЦкжаПМЪдГЩМЈЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪО,ЦфжаГЩМЈЗжзщЧјМфЪЧ![]() ,
,![]() ,
,![]() ,
,![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.
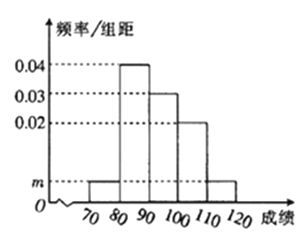
![]() ЧѓЭМжа
ЧѓЭМжа![]() ЕФжЕЃЛ
ЕФжЕЃЛ
![]() ИљОнЦЕТЪЗжВМжБЗНЭМ,ЙРМЦет
ИљОнЦЕТЪЗжВМжБЗНЭМ,ЙРМЦет![]() УћбЇЩњЕФЦНОљЗжЃЛ
УћбЇЩњЕФЦНОљЗжЃЛ
![]() Шєет
Шєет![]() УћбЇЩњЕФЪ§бЇГЩМЈжа,ФГаЉЗжЪ§ЖЮЕФШЫЪ§
УћбЇЩњЕФЪ§бЇГЩМЈжа,ФГаЉЗжЪ§ЖЮЕФШЫЪ§![]() гыгЂгяГЩМЈЯргІЗжЪ§ЖЮЕФШЫЪ§
гыгЂгяГЩМЈЯргІЗжЪ§ЖЮЕФШЫЪ§![]() жЎБШШчБэЫљЪО,ЧѓгЂгяГЩМЈдк
жЎБШШчБэЫљЪО,ЧѓгЂгяГЩМЈдк![]() ЕФШЫЪ§.
ЕФШЫЪ§.
ЗжЪ§ЖЮ |
|
|
|
|
| 1:2 | 1:1 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() ЃЈ
ЃЈ![]() ЁЂ
ЁЂ![]() ЮЊГЃЪ§Чв
ЮЊГЃЪ§Чв![]() ЃЉЃЌТњзуЬѕМў
ЃЉЃЌТњзуЬѕМў![]() ЃЌЧвЗНГЬ
ЃЌЧвЗНГЬ![]() гаЕШИљ.
гаЕШИљ.
ЃЈ1ЃЉШє![]() ЃЌ
ЃЌ![]() КуГЩСЂЃЌЧѓЪЕЪ§
КуГЩСЂЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЪЧЗёДцдкЪЕЪ§![]() ЃЌ
ЃЌ![]() ЃЌЪЙ
ЃЌЪЙ![]() ЕБЖЈвхгђЮЊ
ЕБЖЈвхгђЮЊ![]() ЪБЃЌжЕгђЮЊ
ЪБЃЌжЕгђЮЊ![]() ЃПШчЙћДцдкЃЌЧѓГі
ЃПШчЙћДцдкЃЌЧѓГі![]() ЃЌ
ЃЌ![]() ЕФжЕЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФжЕЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЕФНЙЕуЮЊ
ЕФНЙЕуЮЊ![]() ЃЌШєЙ§
ЃЌШєЙ§![]() ЧвЧуаБНЧЮЊ
ЧвЧуаБНЧЮЊ![]() ЕФжБЯпНЛ
ЕФжБЯпНЛ![]() гк
гк![]() ЃЌ
ЃЌ![]() СНЕуЃЌТњзу
СНЕуЃЌТњзу![]() .
.
ЃЈ1ЃЉЧѓХзЮяЯп![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉШє![]() ЮЊ
ЮЊ![]() ЩЯЖЏЕуЃЌ
ЩЯЖЏЕуЃЌ![]() ЃЌ
ЃЌ![]() дк
дк![]() жсЩЯЃЌдВ
жсЩЯЃЌдВ![]() ФкЧагк
ФкЧагк![]() ЃЌЧѓ
ЃЌЧѓ![]() УцЛ§ЕФзюаЁжЕ.
УцЛ§ЕФзюаЁжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖЈвхгђЮЊRЕФКЏЪ§![]() ЪЧЦцКЏЪ§
ЪЧЦцКЏЪ§
ЃЈ1ЃЉЧѓ![]() ЁЂ
ЁЂ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉХаЖЯ![]() ЕФЕЅЕїадЃЈВЛашвЊжЄУїЃЉЃЌВЂаДГі
ЕФЕЅЕїадЃЈВЛашвЊжЄУїЃЉЃЌВЂаДГі![]() ЕФжЕгђЃЛ
ЕФжЕгђЃЛ
ЃЈ3ЃЉШєЖдШЮвтЕФ![]() ЃЌВЛЕШЪН
ЃЌВЛЕШЪН![]() КуГЩСЂЃЌЧѓЪЕЪ§
КуГЩСЂЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧЙњМЪЬяСЊЕФБъзМ400УзХмЕРЃЌЫќЕФзюФкВрХмЕРЕФБпЯпЪЧгЩСНИљ84.39УзЕФЦНаажБЯпКЭСНЖЮАыОЖ36.80УзЕФАыдВзщГЩЃЌУПИљХмЕРПэ1.22УзЃЈЕРгыЕРМфЕФЛЎЯпПэЖШКіТдВЛМЦЃЉ.БШШќЪБдЫЖЏдБДгЯТЗНБъгаЪ§зжДІГіЗЂ.ЮЊСЫБШйЙЋЦНЃЌЭтЕРЕФдЫЖЏдБЕФЦ№ХмЕуНЯФкЕРЕФЛсгавЛЖЈЕФЬсЧАСПЃЌЪЙЕУЫљгадЫЖЏдБХмЙ§ЕФТЗГЬЭъШЋвЛжТ.МйЩшУПЮЛдЫЖЏдБЖМЛсбизХздМКЕРДЮЕФзюФкВрХм.

ЃЈ1ЃЉЪдИјГі400УзБШШќИїЕРДЮЬсЧАСП![]() ЙигкЕРДЮ
ЙигкЕРДЮ![]() жЎМфЕФКЏЪ§ЙиЯЕЃЌВЂЭъГЩЯТБэЃЈОЋШЗЕН0.01УзЃЉ
жЎМфЕФКЏЪ§ЙиЯЕЃЌВЂЭъГЩЯТБэЃЈОЋШЗЕН0.01УзЃЉ
ЃЈ2ЃЉ800УзБШШќЕФЙцдђЪЧДгГіЗЂДІАДЕРДЮХмЭъЕквЛИіЭфЕРКѓПЩвдПЊЪМВЂЕРШќХмЃЌЧыФуЩшМЦЕк8ЕРбЁЪжЕФзюгХХмВНТЗЯпВЂИјГіЫћЦ№ХмЕФЬсЧАСПгІИУЪЧЖрЩй.
ЕРДЮ | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
ЬсЧАСПЃЈУзЃЉ | 7.67 | 15.33 | 23.00 | 30.66 | 38.33 | 46.00 | 53.66 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈ1ЃЉЬжТлКЏЪ§![]() ЕФЕЅЕїадЃЛ
ЕФЕЅЕїадЃЛ
ЃЈ2ЃЉЕБКЏЪ§![]() гаСНИіСуЕуЃЌЧѓЪЕЪ§
гаСНИіСуЕуЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com