[题目]每到春夏交替时节.雌性杨树会以满天飞絮的方式来传播下一代.漫天飞舞的杨絮易引发皮肤病.呼吸道疾病等.给人们造成困扰.为了解市民对治理杨絮方法的赞同情况.某课题小组随机调査了部分市民.并根据调查结果绘制了尚不完整的统计图表由两个统计图表可以求得.选择D选项的人数和扇形统计图中E的圆心角度数分别为( )A.500.28.8°B.25 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】每到春夏交替时节，雌性杨树会以满天飞絮的方式来传播下一代，漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等，给人们造成困扰，为了解市民对治理杨絮方法的赞同情况，某课题小组随机调査了部分市民（问卷调査表如下表所示），并根据调查结果绘制了尚不完整的统计图表（如下图）

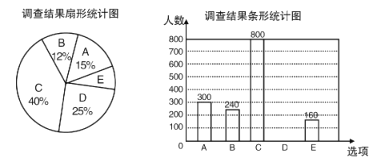
由两个统计图表可以求得，选择D选项的人数和扇形统计图中E的圆心角度数分别为（）

A.500，28.8°B.250，28.6°C.500，28.6°D.250，28.8°

【答案】A

【解析】

根据调查结果条形图中选择A的人数，结合调查结果扇形统计图中选择A的人数的比例求出接受调查市民的总人数，这样可以求出选择D选项的人数，最后根据调查结果扇形统计图求出E的圆心角度数即可.

设接受调查市民的总人数为，由调查结果条形图可知选择A的人数为300，通过调查结果扇形统计图可知：选择A的人数的比例为，因此有，

而选择D选项的人数为：，

扇形统计图中E的圆心角度数为：

故选：A

练习册系列答案

开心15天精彩寒假巧计划江苏凤凰科学技术出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知椭圆的对称中心为原点，焦点在轴上，焦距为，点在该椭圆上．

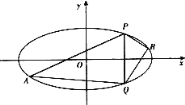
（1）求椭圆的方程；

（2）直线与椭圆交于两点，点位于第一象限，是椭圆上位于直线两侧的动点．当点运动时，满足，问直线的斜率是否为定值，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

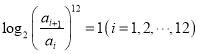【题目】著名物理学家李政道说：“科学和艺术是不可分割的”.音乐中使用的乐音在高度上不是任意定的，它们是按照严格的数学方法确定的.我国明代的数学家、音乐理论家朱载填创立了十二平均律是第一个利用数学使音律公式化的人.十二平均律的生律法是精确规定八度的比例，把八度分成13个半音，使相邻两个半音之间的频率比是常数，如下表所示，其中表示这些半音的频率，它们满足.若某一半音与的频率之比为，则该半音为（）

频率

半音

C（八度）

A.B.GC.D.A

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设函数g(x)=sinωx(ω＞0)向左平移个单位长度得到函数f(x)，已知f(x)在[0，2π]上有且只有5个零点，则下列结论正确的是（）

A.f(x)的图象关于直线对称

B.f(x)在(0，2π)上有且只有3个极大值点，f(x)在(0，2π)上有且只有2个极小值点

C.f(x)在上单调递增

D.ω的取值范围是[)

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数，是f(x)的导函数．

（1）证明：当x＞0时，f(x)＞0；

（2）证明：在()上有且只有3个零点．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数.

（1）若函数的极小值为1，求实数m的值；

（2）若函数在时，其图象全部都在第一象限，求实数m的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在平面直角坐标系中，以原点O为极点，以x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为，直线的参数方程为（t为参数），，点A为直线与曲线C在第二象限的交点，过O点的直线与直线互相垂直，点B为直线与曲线C在第三象限的交点.

（1）写出曲线C的直角坐标方程及直线的普通方程；

（2）若，求的面积.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】为了提高生产线的运行效率，工厂对生产线的设备进行了技术改造．为了对比技术改造后的效果，采集了生产线的技术改造前后各20次连续正常运行的时间长度（单位：天）数据，并绘制了如茎叶图：

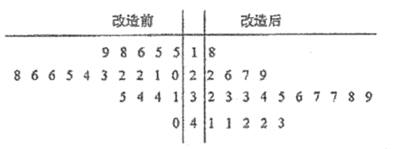
（1）（i）设所采集的40个连续正常运行时间的中位数m，并将连续正常运行时间超过m和不超过m的次数填入下面的列联表：

	超过	不超过
改造前
改造后

（ii）根据（i）中的列联表，能否有99%的把握认为生产线技术改造前后的连续正常运行时间有差异？

附：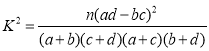

	0.050	0.010	0.001
	3.841	6.635	10.828

（2）工厂的生产线的运行需要进行维护，工厂对生产线的生产维护费用包括正常维护费、保障维护费两种．对生产线设定维护周期为T天（即从开工运行到第kT天进行维护．生产线在一个生产周期内设置几个维护周期，每个维护周期相互独立．在一个维护周期内，若生产线能连续运行，则不会产生保障维护费；若生产线不能连续运行，则产生保障维护费．经测算，正常维护费为0.5万元/次；保障维护费第一次为0.2万元/周期，此后每增加一次则保障维护费增加0.2万元．现制定生产线一个生产周期（以120天计）内的维护方案：，．以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率，求一个生产周期内生产维护费的分布列．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】英国统计学家E．H．辛普森1951年提出了著名的辛普森悖论，下面这个案例可以让我们感受到这个悖论．有甲乙两名法官，他们都在民事庭和行政庭主持审理案件，他们审理的部分案件被提出上诉．记录这些被上述案件的终审结果如下表所示（单位：件）：

法官甲				法官乙
终审结果	民事庭	行政庭	合计	终审结果	民事庭	行政庭	合计
维持	29	100	129	维持	90	20	110
推翻	3	18	21	推翻	10	5	15
合计	32	118	150	合计	100	25	125