分析:(I)利用数列中前n项和Sn与通项an之间的关系,将前n项和Sn转化为通项an之间的关系是解决本题的关键.用等差数列的定义判断该数列是等差数列;
(II)发现数列{bn}的规律是解决本题的关键.转化为等差数列求和问题.
(III)裂项求和是解决本小题的关键.利用放缩法从左边放缩到右边.
解答:解:(I)∵na
n+1=S
n+n(n+1)①∴(n-1)a
n=S
n-1+(n-1)n(n≥2)②
①-②整理得,a
n+1-a
n=2(n≥2)
又由①,取n=1得a
2-a
1=2∴a
n+1-a
n=2(n∈N
*)
∴数列{a
n}是以4为首项,2为公差的等差数列.
(II)由(I)知a
n=4+2(n-1)=2(n+1)
∴b
n+1-b
n=2(n+1)
∴(b
n-b
n-1)+(b
n-1-b
n-2)+…+(b
3-b
2)+(b
2-b
1)=2n+2(n-1)+…+2×3+2×2=n
2+n-2
∴b
n=n(n+1).
(III)由
cn=得,
cn==-∴c
1+c
2+…+c
n=
1-+-+…+-=1-<1.
点评:本题考查等差数列的确定,利用等差数列的定义解决.考查数列中前n项和Sn与通项an之间的关系,考查学生的等价转化思想和化归思想,数列求和的裂项求和方法,证明不等式的放缩法等方法.



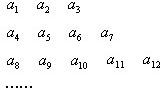 将数列{an}中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表:
将数列{an}中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表: