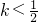已知关于x的不等式k•4x-2x+1+6k<0
(1)若不等式的解集A={x|1<x<log23},求实数k的值;
(2)若不等式的解集A?{x|1<x<log23},求实数k的取值范围;
(3)若不等式的解集A⊆{x|1<x<log23},求实数k的取值范围;
(4)若不等式的解集A∩{x|1<x<log23}≠?,求实数k的取值范围.
解:(1)由已知得,2和3是相应方程kt
2-2t+6k=0的两根且k>0,k=

(2)∵A?{x|1<x<log
23},∴A?{x|2<t<3}且A中的元素t>0
令f(t)=kt
2-2t+6k,
当k>0时,则有 f(2)≤0,f(3)≤0
解得0<k≤

当k=0时,A={t|t>0}显然满足条件
当k<0时,由于x=
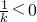
,则只要
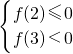
,此时可得k<0
综上可得a
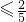
(3)对应方程的△=4-24k
2,令f(t)=kt
2-2t+6k
则原问题等价于△≤0或 f(2)≥0,f(3)≥0,
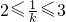
又k>0,∴k≥

由 f(2)≥0,f(3)≥0,2≤

≤3解得

≤k≤

综上,符合条件的k的取值范围是[

,+∞)
(4)当A∩{t|2<t<3}=∅时可得
若k=0,A={t|t>0},符合条件
若k>0可得
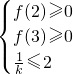
或
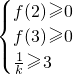
解不等式组可得,
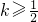
或k不存在
即k

时,A∩{t|2<t<3}=∅
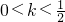
时A∩{t|2<t<3}≠∅
若k<0可得,结合二次函数的图象可知A∩{t|2<t<3}≠∅
综上可得,
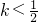
分析:令t=2
x,则原不等式可转化为kt
2-2t+6k<0,由1<x<log
23可得2<t<3
(1)不等式解集区间的端点就是相应方程的根,所以方程kt
2-2t+6k=0的两根分别为2和3,再利用一元二次方程根与系数的关系,可得实数k的值;
(2)函数f(t)=kt
2-2t+6k,分k>0,k=0,k<0三种情况分别进行讨论可得实数k的取值范围
(3)原命题题等价于不等式组:△≤0或 f(2)≥0,f(3)≥02≤1k先解△≤0,可得符合条件的k的取值范围.
(4)由A∩{t|2<t<3}≠∅可得,先寻求A∩{t|2<t<3}=∅的k的范围,再利用补集进行求解
点评:本题考查了一元二次方程根与一元二次不等式的关系,属于中档题.解题时应该注意求解过程中的分类讨论思想与数形结思想的运用.



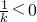 ,则只要
,则只要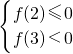 ,此时可得k<0
,此时可得k<0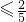
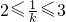

 ≤3解得
≤3解得  ≤k≤
≤k≤
 ,+∞)
,+∞)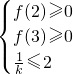 或
或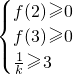
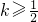 或k不存在
或k不存在 时,A∩{t|2<t<3}=∅
时,A∩{t|2<t<3}=∅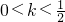 时A∩{t|2<t<3}≠∅
时A∩{t|2<t<3}≠∅