练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （5分）（2011•湖北）某市有大型超市200家、中型超市400家、小型超市1400家．为掌握各类超市的营业情况，现按分层抽样方法抽取一个容量为100的样本，应抽取中型超市          家．

    20

    解析试题分析：根据所给的三种超市的数目，相加得到共有的超市数目，根据要抽取的超市数目，得到每个个体被抽到的概率，用中等超市的数目乘以被抽到的概率，得到结果．
    解：∵大型超市200家、中型超市400家、小型超市1400家，
    ∴共有超市200+400+1400=2000，
    ∵按分层抽样方法抽取一个容量为100的样本，
    ∴每个个体被抽到的概率是，
    ∴中型超市要抽取400×=20家，
    故答案为：20．
    点评：本题考查分层抽样，这是一个每年必考的题目，解题的关键是抽样过程中每个个体被抽到的概率相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    以下结论正确的是        
    （1）根据2×2列联表中的数据计算得出2≥6.635, 而P（2≥6.635）≈0.01，则有99% 的把握认为两个分类变量有关系。
    （2）在线性回归分析中，相关系数为r，|r|越接近于1，相关程度越大；|r|越小，相关程度越小。
    （3）在回归分析中，回归直线方程过点。 
    （4）在回归直线中，变量x=200时，变量y的值一定是15。

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知一个样本容量为的样本数据的频率分布直方图如图所示，那么样本数据落在[40,60）内的样本的频数为     ____ ；估计总体的众数为_________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知x与y之间的一组数据：

    则y与x的线性回归方程为y=bx+a必过点        ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    某工厂甲、乙、丙三个车间生产同一产品，数量分别为120件，90件，60
    件. 为了解它们的产品质量是否有显著差异，用分层抽样方法抽取了一个容量
    为的样本进行调查，其中从丙车间的产品中抽取了4件，则       ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    某市教育局为了调查学生每周零花钱的数量（钱数取整数元），以便引导学生树立正确的消费观，从该市24000名学生中随机抽取1000名调查，根据所得数据绘得频率分布直方图如图所示，则
    （1）样本数据落在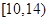内的频数为        ；
    （2）若每周零花钱数量在10元以下为“有节约习惯”标准，则该市“有节约习惯”的学生数大约为    ．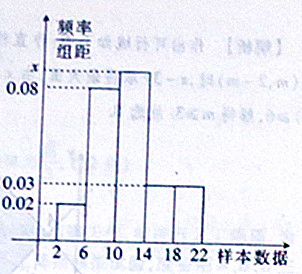

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    计算下面事件A与事件B的2×2列联表的χ2统计量值，得χ2≈________，从而得出结论________.

     
    		B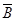

    		总计
    A
    		39
    		157
    		196

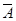    		29
    		167
    		196
    总计
    		68
    		324
    		392

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    (2014·嘉兴模拟)在一次运动员的选拔中,测得7名选手身高(单位：cm)分布的茎叶图如图所示.已知记录的平均身高为164cm,但有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为__________.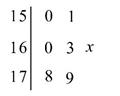

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    某校举行了由全部学生参加的校园安全知识考试，从中抽出60名学生，将其成绩分成六段[40,50)，[50, 60)，…，[90,100]后，画出如图所示的频率分布直方图．观察图形的信息，回答下列问题：估计这次考试的及格率(60分及以上为及格)为________；平均分为________．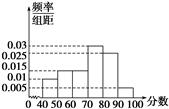

    查看答案和解析>>

    同步练习册答案