
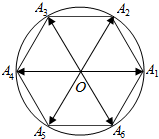
 已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$.
已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$. 分析 设点P位于弧$\widehat{{A}_{1}{A}_{2}}$上时,设∠POA1=α,当$0≤α<\frac{π}{6}$时,则θ1=α,θ2=$\frac{π}{3}$-α,θ3=$\frac{2π}{3}$-α,θ4=π-α,θ5=$α+\frac{2π}{3}$,θ6=$α+\frac{π}{3}$.将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,α,$\frac{π}{3}$-α,$α+\frac{π}{3}$,$\frac{2π}{3}$-α,$α+\frac{2π}{3}$,π-α,利用等差数列的性质即可得出.
解答 解:设点P位于弧$\widehat{{A}_{1}{A}_{2}}$上时,设∠POA1=α,当$0≤α<\frac{π}{6}$时,则θ1=α,θ2=$\frac{π}{3}$-α,θ3=$\frac{2π}{3}$-α,θ4=π-α,θ5=$α+\frac{2π}{3}$,θ6=$α+\frac{π}{3}$.
将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,α,$\frac{π}{3}$-α,$α+\frac{π}{3}$,$\frac{2π}{3}$-α,$α+\frac{2π}{3}$,π-α,
由2($\frac{π}{3}$-α)=α+$α+\frac{π}{3}$,解得α=$\frac{π}{12}$,此时六个角分别为:$\frac{π}{12}$,$\frac{3π}{12}$,$\frac{5π}{12}$,$\frac{7π}{12}$,$\frac{9π}{12}$,$\frac{11π}{12}$,成等差数列,
则该等差数列的第3项为 $\frac{5π}{12}$.
其它情况类比可得.
故答案为:$\frac{5π}{12}$.
点评 本题考查了向量的夹角、等差数列的通项公式及其性质,考查了分类讨论方法、类比推理与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 若m∥n,n?α,则m∥α | B. | 若m∥α,n?α,则m∥n | C. | 若m⊥n,n?α,则m⊥α | D. | 若m⊥α,m∥n,则n⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com