
(本小题满分12分)
已知数列 的前
的前 项和为
项和为 ,满足
,满足 .
.
(1)求证:数列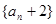 为等比数列;
为等比数列;
(2)若数列 满足
满足 ,
, 为数列
为数列 的前
的前 项和,求证:
项和,求证: .
.
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:解答题
已知数列 是等差数列,
是等差数列,
(1)判断数列 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;
(2)如果 ,试写出数列
,试写出数列 的通项公式;
的通项公式;
(3)在(2)的条件下,若数列 得前n项和为
得前n项和为 ,问是否存在这样的实数
,问是否存在这样的实数 ,使
,使 当且仅当
当且仅当 时取得最大值。若存在,求出
时取得最大值。若存在,求出 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 ,数列
,数列 满足
满足 ,数列
,数列 满足
满足 ;又知数列
;又知数列 中,
中, ,且对任意正整数
,且对任意正整数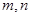 ,
, .
.
(Ⅰ)求数列 和数列
和数列 的通项公式;
的通项公式;
(Ⅱ)将数列 中的第
中的第 项,第
项,第 项,第
项,第 项,……,第
项,……,第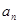 项,……删去后,剩余的项按从小到大的顺序排成新数列
项,……删去后,剩余的项按从小到大的顺序排成新数列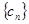 ,求数列
,求数列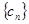 的前
的前 项和.
项和.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
在数列{an}中,a1=1,an=n2[1+ +
+ +…+
+…+ ] (n≥2,n∈N)
] (n≥2,n∈N)
(1)当n≥2时,求证: =
=
(2)求证:(1+ )(1+
)(1+ )…(1+
)…(1+ )<4
)<4
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)已知数列 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为 ,
, 为其前
为其前 项和,且满足
项和,且满足 ,
, .数列
.数列 满足
满足 ,
, 为数列
为数列 的前n项和.
的前n项和.
(Ⅰ)求数列 的通项公式
的通项公式 和数列
和数列 的前n项和
的前n项和 ;
;
(Ⅱ)若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com