
已知函数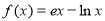 ,
,
(1)求函数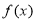 的单调区间;
的单调区间;
(2)在区间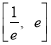 内存在
内存在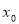 ,使不等式
,使不等式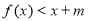 成立,求
成立,求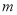 的取值范围.
的取值范围.
(1)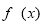 的单调递增区间是
的单调递增区间是 ,
,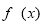 的单调递减区间是
的单调递减区间是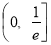 .
.
(2)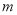 的取值范围是
的取值范围是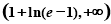 .
.
【解析】
试题分析:(1)首先确定函数的定义域.求导数:
 ,根据当
,根据当 时,
时,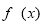 为单调递增函数;
为单调递增函数;
当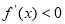 时,
时,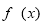 为单调递减函数,得到函数的单调区间.
为单调递减函数,得到函数的单调区间.
(2)构造函数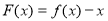 ,即
,即 ,将问题转化成:在区间
,将问题转化成:在区间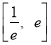 内,
内, ,利用导数求函数的极值、最小值,得到
,利用导数求函数的极值、最小值,得到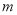 的取值范围是
的取值范围是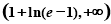 .
.
试题解析:(1)函数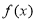 的定义域为
的定义域为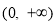 ,
,
 2分
2分
当 ,即
,即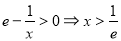 时,
时,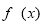 为单调递增函数;
为单调递增函数;
当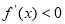 ,即
,即 时,
时,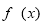 为单调递减函数;
为单调递减函数;
所以,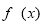 的单调递增区间是
的单调递增区间是 ,
,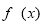 的单调递减区间是
的单调递减区间是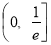 6分
6分
(2)由不等式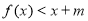 ,得
,得 ,令
,令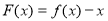 ,
,
则 8分
8分
由题意可转化为:在区间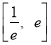 内,
内, ,
,
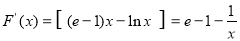 ,令
,令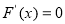 ,得
,得
|
|
|
|
|
|
|
|
|
0 |
+ |
|
|
| 递减 | 极小值 | 递增 |
|
由表可知: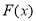 的极小值是
的极小值是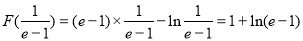 且唯一,
且唯一,
所以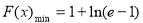 。 10分
。 10分
因此,所求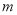 的取值范围是
的取值范围是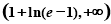 . 13分
. 13分
考点:应用导数研究函数的单调性、极值、最值


科目:高中数学 来源:2013-2014学年广东省东莞市高三模拟(一)文科数学试卷(解析版) 题型:选择题
定义某种运算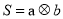 ,运算原理如上图所示,则式子
,运算原理如上图所示,则式子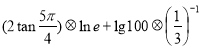 的值为( )
的值为( )
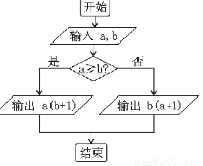
A.4 B.8 C.11 D.13
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省青岛市高三4月统一质量检测考试文科数学试卷(解析版) 题型:选择题
某防疫站对学生进行身体健康调查,欲采用分层抽样的办法抽取样本.某中学共有学生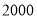 名,抽取了一个容量为
名,抽取了一个容量为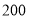 的样本,已知样本中女生比男生少
的样本,已知样本中女生比男生少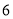 人,则该校共有女生( )
人,则该校共有女生( )
A.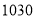 人 B.
人 B.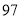 人 C.
人 C.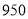 人 D.
人 D.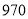 人
人
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省高三12月月考理科数学试卷(解析版) 题型:选择题
已知命题p1:函数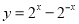 在R上为增函数,p2:函数
在R上为增函数,p2:函数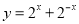 在R上为减函数,则在命题
在R上为减函数,则在命题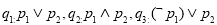 和
和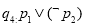 中,真命题是 ( )
中,真命题是 ( )
A.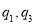 B.
B.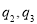 C.
C.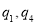 D.
D.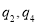
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省高三12月月考文科数学试卷(解析版) 题型:解答题
设命题p:函数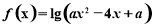 的定义域为R;
的定义域为R;
命题q:不等式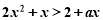 ,对
,对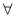
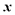 ∈(-∞,-1)上恒成立,
∈(-∞,-1)上恒成立,
如果命题“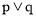 ”为真命题,命题“
”为真命题,命题“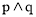 ”为假命题,求实数
”为假命题,求实数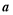 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省高三12月月考文科数学试卷(解析版) 题型:选择题
三棱柱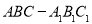 的侧棱长和底面边长均为
的侧棱长和底面边长均为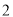 ,且侧棱
,且侧棱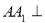 底面
底面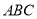 ,其正视图是边长为
,其正视图是边长为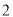 的正方形,则此三棱柱侧视图的面积为( )
的正方形,则此三棱柱侧视图的面积为( )
A.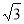 B.
B.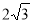 C.
C. 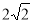 D.
D.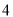
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省菏泽市高三3月模拟考试理科数学试卷(解析版) 题型:填空题
如图,A是半径为5的圆O上的一个定点,单位向量 在A点处与圆O 相切,点P是圆O上的一个动点,且点P与点A不重合,则
在A点处与圆O 相切,点P是圆O上的一个动点,且点P与点A不重合,则 ·
· 的取值范围是 .
的取值范围是 .

查看答案和解析>>
科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考文科数学试卷(解析版) 题型:解答题
已知函数f(x)=ax+x2-xlna(a>0,a≠1).
(1)当a>1时,求证:函数f(x)在(0,+∞)上单调递增;
(2)若函数y=|f(x)-t|-1有三个零点,求t的值;
(3)若存在x1,x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1,试求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com