
【题目】已知数列![]() 满足
满足![]()
![]() ,
, ![]() 是数列
是数列![]() 的前
的前![]() 项和.
项和.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)令![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() 是以
是以![]() 为首项,2为公差的等差数列 (2)
为首项,2为公差的等差数列 (2)![]()
【解析】试题分析:(1)由 ![]() 可得
可得![]() ,两式相减可得
,两式相减可得![]() ,由等差数列可得结果;(2)由1) 可得
,由等差数列可得结果;(2)由1) 可得![]() ,根据错位相减法可得数列
,根据错位相减法可得数列![]() 的前
的前![]() 项和
项和![]() .
.
试题解析:(1)![]() ....................... ①
....................... ①
![]() 时,
时, ![]() ………………. ②
………………. ②
①-②得![]() ,
,
从而![]()
又![]() 时,
时, ![]()
因此,数列![]() 是以
是以![]() 为首项,2为公差的等差数列.
为首项,2为公差的等差数列.
![]()
(2)![]()
![]() ……………. ③
……………. ③
![]() ……… ④
……… ④
③-④得![]()
整理得 ![]()
【 方法点睛】本题主要考查等比数列和等差数列的通项以及错位相减法求数列的的前![]() 项和,属于中档题.一般地,如果数列
项和,属于中档题.一般地,如果数列![]() 是等差数列,
是等差数列, ![]() 是等比数列,求数列
是等比数列,求数列![]() 的前
的前![]() 项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列
项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列![]() 的公比,然后作差求解, 在写出“
的公比,然后作差求解, 在写出“![]() ”与“
”与“![]() ” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“
” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“![]() ”的表达式.
”的表达式.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】为了研究某学科成绩(满分100分)是否与学生性别有关,采用分层抽样的方法,从高二年级抽取了30名男生和20名女生的该学科成绩,得到下图所示女生成绩的茎叶图.其中抽取的男生中有21人的成绩在80分以下,规定80分以上为优秀(含80分).
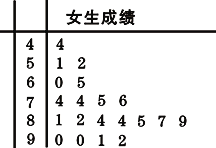
(1)请根据题意,将2×2列联表补充完整;
优秀 | 非优秀 | 总计 | |
男生 | |||
女生 | |||
总计 | 50 |
(2)据此列联表判断,是否有90%的把握认为该学科成绩与性别有关?
附: 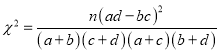 ,其中
,其中![]() .
.
参考数据 | 当 |
当 | |
当 | |
当 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在[-1,1]上的奇函数f(x),已知当x∈[-1,0]时,f(x)=![]() -
-![]() (a∈R).
(a∈R).
(1)写出f(x)在[0,1]上的解析式;
(2)求f(x)在[0,1]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如下表:
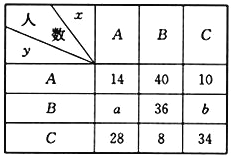
若抽取学生![]() 人,成绩分为
人,成绩分为![]() (优秀),
(优秀),![]() (良好),
(良好),![]() (及格)三个等次,设
(及格)三个等次,设![]() 分别表示数学成绩与地理成绩,例如:表中地理成绩为
分别表示数学成绩与地理成绩,例如:表中地理成绩为![]() 等级的共有
等级的共有![]() (人),数学成绩为
(人),数学成绩为![]() 等级且地理成绩为
等级且地理成绩为![]() 等级的共有8人.已知
等级的共有8人.已知![]() 与
与![]() 均为
均为![]() 等级的概率是
等级的概率是![]() .
.
(1)设在该样本中,数学成绩的优秀率是![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,
,![]() ,求数学成绩为
,求数学成绩为![]() 等级的人数比
等级的人数比![]() 等级的人数多的概率.
等级的人数多的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果存在函数![]() (
(![]() 为常数),使得对函数
为常数),使得对函数![]() 定义域内任意
定义域内任意![]() 都有
都有![]() 成立,那么称
成立,那么称![]() 为函数
为函数![]() 的一个“线性覆盖函数”.给出如下四个结论:
的一个“线性覆盖函数”.给出如下四个结论:
①函数![]() 存在“线性覆盖函数”;
存在“线性覆盖函数”;
②对于给定的函数![]() ,其“线性覆盖函数”可能不存在,也可能有无数个;
,其“线性覆盖函数”可能不存在,也可能有无数个;
③![]() 为函数
为函数![]() 的一个“线性覆盖函数”;
的一个“线性覆盖函数”;
④若![]() 为函数
为函数![]() 的一个“线性覆盖函数”,则
的一个“线性覆盖函数”,则![]()
其中所有正确结论的序号是___________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com