练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知数列的各项均为正数，前项和为，且.

    （1）求证：数列是等差数列；

    （2）若数列满足，求证： .

    【答案】（1）证明见解析；（2）证明见解析

    【解析】试题分析：（1）由可得，两式相减，化简可得， ，从而可得数列是等差数列；；（2）由（1）得,利用裂项相消法求和后，根据放缩法可证明结论.

    试题解析：（1）时， ，且，故

    时，

    整理得

    即

    所以数列是以为首项， 为公差的等差数列.

    （2）由（1）得

    故.

    【方法点晴】本题主要考查递推公式、等差数列的通项与求和公式，以及裂项相消法求数列的和，属于中档题. 裂项相消法是最难把握的求和方法之一，其原因是有时很难找到裂项的方向，突破这一难点的方法是根据式子的结构特点，常见的裂项技巧：(1) ；（2） ； （3）；（4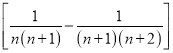） ；此外，需注意裂项之后相消的过程中容易出现丢项或多项的问题，导致计算结果错误.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】函数f（x2）的定义域为（﹣3，1]，则函数f（x﹣1）的定义域为（ ）
    A.[2，10）
    B.[1，10）
    C.[1，2]
    D.[0，2]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=cos4x﹣2sinxcosx﹣sin4x．
    （1）求f（x）的最小正周期；
    （2）求f（x）的单调增区间；
    （3）若 ，求f（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】求函数f（x）=﹣x2+4x﹣6，x∈[0，5]的值域（ ）
    A.[﹣6，﹣2]
    B.[﹣11，﹣2]
    C.[﹣11，﹣6]
    D.[﹣11，﹣1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在平面直角坐标系内，点 在曲线：，（为参数，）上运动，以为极轴建立极坐标系.直线的极坐标方程为.

    (Ⅰ)写出曲线的标准方程和直线的直角坐标方程；

    (Ⅱ)若直线与曲线相交于两点，点在曲线上移动，求面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数和（为常数）的图象在处有公切线.

    （Ⅰ）求实数的值；

    （Ⅱ）求函数的极大值和极小值；

    （Ⅲ）关于x的方程由几个不同的实数解？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】圆截直线所得弦长为2，则实数__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】根据以往的经验，某工程施工期间的将数量X（单位：mm）对工期的影响如下表：

    降水量X

    X＜300

    300≤X＜700

    700≤X＜900

    X≥900

    工期延误天数Y

    0

    2

    6

    10

    历年气象资料表明，该工程施工期间降水量X小于300，700，900的概率分别为0.3，0.7，0.9，求：
    （1）工期延误天数Y的均值与方差；
    （2）在降水量X至少是300的条件下，工期延误不超过6天的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在极坐标系中，圆的极坐标方程为，若以极点为原点，极轴所在的直线为轴建立平面直角坐标系.

    （1）求圆的参数方程；

    （2）在直线坐标系中，点是圆上的动点，试求的最大值，并求出此时点的直角坐标.

    查看答案和解析>>

    同步练习册答案