
【题目】据历年大学生就业统计资料显示:某大学理工学院学生的就业去向涉及公务员、教师、金融、公司和自主创业等五大行业2020届该学院有数学与应用数学、计算机科学与技术和金融工程等三个本科专业,毕业生人数分别是70人,140人和210人现采用.分层抽样的方法,从该学院毕业生中抽取18人调查学生的就业意向.
(1)应从该学院三个专业的毕业生中分别抽取多少人?
(2)国家鼓励大学生自主创业,在抽取的18人中,就业意向恰有三个行业的学生有5人为方便统计,将恰有三个行业就业意向的这5名学生分别记为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,统计如下表:
,统计如下表:
|
|
|
|
| |
公务员 | ○ | ○ | × | ○ | × |
教师 | ○ | × | ○ | × | ○ |
金融 | ○ | ○ | ○ | × | ○ |
公式 | × | × | ○ | ○ | ○ |
自主创业 | × | ○ | ○ | × |
其中“○”表示有该行业就业意向,“×”表示无该行业就业意向.
现从![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 这5人中随机抽取2人接受采访.设
这5人中随机抽取2人接受采访.设![]() 为事件“抽取的2人中至少有一人有自主创业意向”,求事件
为事件“抽取的2人中至少有一人有自主创业意向”,求事件![]() 发生的概率.
发生的概率.
【答案】(1)分别抽取3人,6人,9人(2)![]()
【解析】
(1)由已知,数学与应用数学、计算机科学与技术和金融工程三个专业的毕业学生之比为1:2:3,采用分层抽样的方法分别计算即可.
(2)用列举法得到从![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 这5人中随机抽取2人接受采访的情况有10种,然后列举出事件
这5人中随机抽取2人接受采访的情况有10种,然后列举出事件![]() 所包含的结果,由古典概率的计算公式可得答案.
所包含的结果,由古典概率的计算公式可得答案.
(1)由己知,数学与应用数学、计算机科学与技术和金融工程三个专业的毕业生人数之比为1:2:3.由于采取分层抽样的方法抽取18人因此应从数学与应用数学、计算机科学与技术和金融工程三个专业分别抽取3人,6人,9人.
(2)从这5个人中随机抽取2人的所有结果有:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,共10种
,共10种
由统计表可知,事件![]() 包含的结果有:
包含的结果有:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共7种
,共7种
所以事件![]() 发生的概率为
发生的概率为![]() .
.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】某调查机构为了了解某产品年产量x(吨)对价格y(千克/吨)和利润z的影响,对近五年该产品的年产量和价格统计如下表:
x | 1 | 2 | 3 | 4 | 5 |
y | 17.0 | 16.5 | 15.5 | 13.8 | 12.2 |
(1)求y关于x的线性回归方程![]() ;
;
(2)若每吨该产品的成本为12千元,假设该产品可全部卖出,预测当年产量为多少时,年利润w取到最大值?
参考公式: 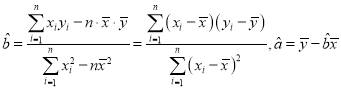
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的浦丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计![]() 的值:先请全校
的值:先请全校![]() 名同学每人随机写下一个都小于
名同学每人随机写下一个都小于![]() 的正实数对
的正实数对![]() ;再统计两数能与
;再统计两数能与![]() 构成钝角三角形三边的数对
构成钝角三角形三边的数对![]() 的个数
的个数![]() ;最后再根据统计数
;最后再根据统计数![]() 估计
估计![]() 的值,那么可以估计
的值,那么可以估计![]() 的值约为( )
的值约为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达
到达![]() 的位置,得到如图所示的四棱锥
的位置,得到如图所示的四棱锥![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
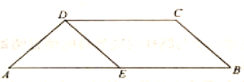
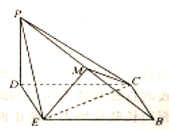
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的左、右焦点分别是
)的左、右焦点分别是![]() ,
,![]() ,点
,点![]() 为
为![]() 的上顶点,点
的上顶点,点![]() 在
在![]() 上,
上,![]() ,且
,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)已知过原点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,垂直于
两点,垂直于![]() 的直线
的直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于
交于![]() ,
,![]() 两点,若
两点,若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月4日的每天昼夜温度与实验室每天每100颗种子中的发芽数,得到如下数据:
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 |
温差 | 11 | 13 | 12 | 8 |
发芽数(颗) | 26 | 32 | 26 | 17 |
根据表中12月1日至12月3日的数据,求得线性回归方程![]() 中的
中的![]() ,则求得的
,则求得的![]() _____;若用12月4日的数据进行检验,检验方法如下:先用求得的线性回归方程计算发芽数
_____;若用12月4日的数据进行检验,检验方法如下:先用求得的线性回归方程计算发芽数![]() ,再求
,再求![]() 与实际发芽数
与实际发芽数![]() 的差,若差值的绝对值不超过2颗,则认为得到的线性回归方程是可靠的,则求得的线性回归方程_____(填“可靠”或“不可靠”).
的差,若差值的绝对值不超过2颗,则认为得到的线性回归方程是可靠的,则求得的线性回归方程_____(填“可靠”或“不可靠”).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于点
于点![]() (点
(点![]() 在
在![]() 轴上方),斜率为
轴上方),斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,且
,且![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)设椭圆![]() 的离心率为
的离心率为![]() ,当点
,当点![]() 为椭圆
为椭圆![]() 的右顶点时,
的右顶点时,![]() 的坐标为
的坐标为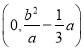 ,求
,求![]() 的值.
的值.
(2)若椭圆![]() 的方程为
的方程为![]() ,且
,且![]() ,是否存在
,是否存在![]() 使得
使得![]() 成立?如果存在,求出
成立?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】光伏发电是将光能直接转变为电能的一种技术,具有资源的充足性及潜在的经济性等优点,在长期的能源战略中具有重要地位,2015年起,国家能源局、国务院扶贫办联合在6省的30个县开展光伏扶贫试点,在某县居民中随机抽取50户,统计其年用量得到以下统计表.以样本的频率作为概率.
用电量(单位:度) |
|
|
|
|
|
户数 | 7 | 8 | 15 | 13 | 7 |
(Ⅰ)在该县居民中随机抽取10户,记其中年用电量不超过600度的户数为![]() ,求
,求![]() 的数学期望;
的数学期望;
(Ⅱ)在总结试点经验的基础上,将村级光伏电站稳定为光伏扶贫的主推方式.已知该县某自然村有居民300户.若计划在该村安装总装机容量为300千瓦的光伏发电机组,该机组所发电量除保证该村正常用电外,剩余电量国家电网以0.8元/度的价格进行收购.经测算每千瓦装机容量的发电机组年平均发电1000度,试估计该机组每年所发电量除保证正常用电外还能为该村创造直接受益多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线E![]() 的左、右焦点分别为F1,F2,P是双曲线E上的一点,且|PF2|=2|PF1|,若直线PF2与双曲线E的渐近线交于点M,且M为PF2的中点,则双曲线E的渐近线方程为( )
的左、右焦点分别为F1,F2,P是双曲线E上的一点,且|PF2|=2|PF1|,若直线PF2与双曲线E的渐近线交于点M,且M为PF2的中点,则双曲线E的渐近线方程为( )
A.y=±![]() B.y=±
B.y=±![]() C.y=±2xD.y=±3x
C.y=±2xD.y=±3x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com