练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

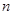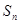    已知数列的各项均不等于0和1，此数列前项的和为，且满足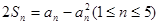，则满足条件的数列共有（    ）

    A.  2个    B.  6个     C.  8个    D.  16个

     

    【答案】

    B

    【解析】解：∵2Sn=an-an2

    ∴2a1=a1-a12

    ∵数列中不存在1和0，

    ∴a1=-1

    2（a1+a2）=a2+a22，解得a2=-2

    同理可得a3=-3或者2，

    当a3=-3时， a4=3，a5=-1± 7 ；

    当a3=-3时，a4=-4时，a5=-1± 11 ；

    当a3=2时，a4=-2，a5=-1± 7 ；

    综合得满足条件的数列共有6个

    故选B

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知数列{an}各项均不为0，其前n项和为Sn，且对任意n∈N*都有（1-p）Sn=p-pan（p为大于1的常数），则an=（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知数列{an}各项均不为0，其前n项和为Sn，且对任意n∈N*都有（1-p）Sn=p-pan（p为大于1的常数），记f(n)=
    1+
    C
    1
    n
    a1+
    C
    2
    n
    a2+…+
    C
    n
    n
    an
    2nSn
    ．
    （1）求an；
    （2）试比较f（n+1）与
    p+1
    2p
    f(n)    的大小（n∈N*）；
    （3）求证：(2n-1)f(n)≤f(1)+f(2)+…+f(2n-1)≤
    p+1
    p-1
    [1-(
    p+1
    2p
    )    2n-1    ]    ，（n∈N*）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知数列{an}各项均不为0，其前n项和为Sn，且对任意n∈N*都有（1-p）Sn=p-pan（p≠±1的常数），记f(n)=
    1+
    C
    1
    n
    a1+
    C
    2
    n
    a2+…+
    C
    n
    n
    an
    2nSn
    ．
    （Ⅰ）求an；
    （Ⅱ）求
    lim
    n→∞
    f(n+1)
    f(n)
    ；
    （Ⅲ）当p＞1时，设bn=
    p+1
    2p
    -
    f(n+1)
    f(n)
    ，求数列{pk+1bkbk+1}的前n项和．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年辽宁沈阳二中等重点中学协作体高三领航高考预测十二理数学卷（解析版） 题型：选择题

    已知数列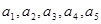的各项均不等于0和1，此数列前项的和为，且满足，则满足条件的数列共有（   ）

    A． 2个             B． 6个             C． 8个             D． 16个

     

    查看答案和解析>>

    同步练习册答案