
【题目】将函数f(x)=sinx的图象向右平移 ![]() 个单位后得到函数y=g(x)的图象,则函数y=f(x)+g(x)的最大值为 .
个单位后得到函数y=g(x)的图象,则函数y=f(x)+g(x)的最大值为 .
 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】下列命题中,正确命题的序号是____________。
①数列{an}的前n项和![]() ,则数列{ an }是等差数列。
,则数列{ an }是等差数列。
②若等差数列{ an }中,已知![]()
![]()
![]() ,则
,则![]()
![]()
③函数![]() 的最小值为2。
的最小值为2。
④等差数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() ,
,![]() ,则
,则![]() 最大时
最大时![]() 13
13
⑤若数列{an}是等比数列,其前n项和为![]() 则常数k的值为1.
则常数k的值为1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C的内角对边分别为a,b,c,满足(a+b+c)(a﹣b+c)=ac.
(1)求B.
(2)若sinAsinC= ![]() ,求C.
,求C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表:
商店名称 |
|
|
|
|
|
销售额 | 3 | 5 | 6 | 7 | 9 |
利润额 | 2 | 3 | 3 | 4 | 5 |
(1)画出销售额和利润额的散点图;
(2)若销售额和利润额具有相关关系,用最小二乘法计算利润额![]() 对销售额
对销售额![]() 的回归直线方程;
的回归直线方程;
(3)据(2)的结果估计当销售额为4千万元时的利润额.
(附:线性回归方程:![]() ,
, ,
,![]() ,)
,)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,D为边BC上一点,AD=6,BD=3, DC=2.
(1)若AD⊥BC,求∠BAC的大小;
(2)若∠ABC= ![]() ,求△ADC的面积.
,求△ADC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设X~N(1,σ2),其正态分布密度曲线如图所示,且P(X≥3)=0.0228,那么向正方形OABC中随机投掷10000个点,则落入阴影部分的点的个数的估计值为( )
(附:随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ<ξ<μ+σ)=68.26%,P(μ-2σ<ξ<μ+2σ)=95.44%)
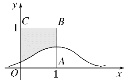
A. 6038 B. 6587 C. 7028 D. 7539
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔业公司年初用81万元购买一艘捕鱼船,第一年各种费用为1万元,以后每年都增加2万元,每年捕鱼收益30万元.
![]() 问第几年开始获利?
问第几年开始获利?
![]() 若干年后,有两种处理方案:方案一:年平均获利最大时,以46万元出售该渔船;
若干年后,有两种处理方案:方案一:年平均获利最大时,以46万元出售该渔船;
方案二:总纯收入获利最大时,以10万元出售该渔船![]() 问:哪一种方案合算?请说明理由.
问:哪一种方案合算?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知![]() ,
,![]() ,且函数
,且函数![]() 的图像上的任意两条对称轴之间的距离的最小值是
的图像上的任意两条对称轴之间的距离的最小值是![]() .
.
(1)求![]() 的值:
的值:
(2)将函数![]() 的图像向右平移
的图像向右平移![]() 单位后,得到函数
单位后,得到函数![]() 的图像,求函数
的图像,求函数![]() 在
在![]() 上的最值,并求取得最值时的
上的最值,并求取得最值时的![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com