
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
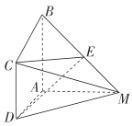
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】已知离心率为![]() 的椭圆
的椭圆![]() 的短轴的两个端点分别为
的短轴的两个端点分别为![]() 、
、![]() ,
,![]() 为椭圆
为椭圆![]() 上异于
上异于![]() 、
、![]() 的动点,且
的动点,且![]() 的面积最大值为
的面积最大值为![]() .
.
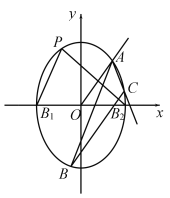
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)射线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,过点
,过点![]() 作倾斜角互补的两条直线,它们与椭圆的另一个交点分别为点
作倾斜角互补的两条直线,它们与椭圆的另一个交点分别为点![]() 和点
和点![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校近几年来通过“书香校园”主题系列活动,倡导学生整本阅读纸质课外书籍.下面的统计图是该校2013年至2018年纸质书人均阅读量的情况,根据统计图提供的信息,下列推断不合理的是( )
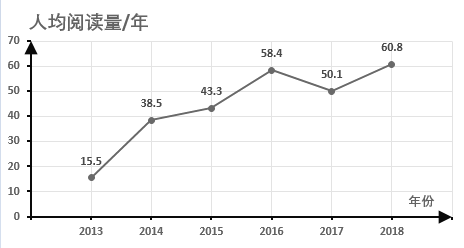
A.从2013年到2016年,该校纸质书人均阅读量逐年增长
B.2013年至2018年,该校纸质书人均阅读量的中位数是46.7本
C.2013年至2018年,该校纸质书人均阅读量的极差是45.3本
D.2013年至2018年,该校后三年纸质书人均阅读量总和是前三年纸质书人均阅读量总和的2倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,PA∥CE,AB=CE![]() PA,PA⊥平面ABCD.
PA,PA⊥平面ABCD.
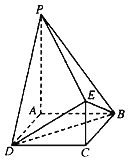
(1)证明:PE⊥平面DBE;
(2)求二面角B﹣PD﹣E的正弦值的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某小区有一块矩形地块![]() ,其中
,其中![]() ,
,![]() ,单位:百米.已知
,单位:百米.已知![]() 是一个游泳池,计划在地块
是一个游泳池,计划在地块![]() 内修一条与池边
内修一条与池边![]() 相切于点
相切于点![]() 的直路
的直路![]() (宽度不计),交线段
(宽度不计),交线段![]() 于点
于点![]() ,交线段
,交线段![]() 于点
于点![]() .现以点
.现以点![]() 为坐标原点,以线段
为坐标原点,以线段![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系,若池边
轴,建立平面直角坐标系,若池边![]() 满足函数
满足函数![]() 的图象,若点
的图象,若点![]() 到
到![]() 轴距离记为
轴距离记为![]() .
.
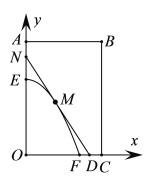
(1)当![]() 时,求直路所在的直线方程;
时,求直路所在的直线方程;
(2)当![]() 为何值时,地块
为何值时,地块![]() 在直路
在直路![]() 不含泳池那侧的面积取到最大,最大值时多少?
不含泳池那侧的面积取到最大,最大值时多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列4个说法中正确的有( )
①命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() 则
则![]() ”;
”;
②若![]() ,则
,则![]() ;
;
③若复合命题:“![]() ”为假命题,则p,q均为假命题;
”为假命题,则p,q均为假命题;
④“![]() ”是“
”是“![]() ”的充分不必要条件.
”的充分不必要条件.
A.①②③B.②③④C.①②④D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com