
【题目】已知函数![]()
(Ⅰ)当a=﹣2时,求函数f(x)的单调区间;
(Ⅱ)若g(x)= ![]() +
+![]() 在
在![]() 1,+∞)上是单调函数,求实数a的取值范围.
1,+∞)上是单调函数,求实数a的取值范围.
【答案】(Ⅰ)![]() 的单调递增区间是(1,+∞),
的单调递增区间是(1,+∞), ![]() 的单调递减区间是(0, 1).
的单调递减区间是(0, 1).
(Ⅱ)实数a的取值范围![]() 0,+∞)
0,+∞)
【解析】试题分析:(Ⅰ)求导函数,利用导数的正负,可得函数的单调递增区间与单调递减区间;(Ⅱ)由题意得![]() ,分函数g(x)为[1,+∞)上的单调增函数与单调减函数讨论,即可确定实数a的取值范围
,分函数g(x)为[1,+∞)上的单调增函数与单调减函数讨论,即可确定实数a的取值范围
试题解析:(1)由已知,函数的定义域为(0,+∞).
当a=-2时,f(x)=x2-2lnx,所以f′(x)=2x-![]() =
=![]() ,
,
则当x∈(0,1)时,f′(x)<0,所以(0,1)为f(x)的单调递减区间.
当x∈(1,+∞)时,f′(x)>0,(1,+∞)为f(x)的单调递增区间.
(2)由题意得g′(x)=2x+![]() -
-![]() ,函数g(x)在[1,+∞)上是单调函数.
,函数g(x)在[1,+∞)上是单调函数.
(ⅰ)若函数g(x)为[1,+∞)上的单调增函数,
则g′(x)≥0在[1,+∞)上恒成立,即a≥![]() -2x2在[1,+∞)上恒成立,
-2x2在[1,+∞)上恒成立,
设φ(x)=![]() -2x2,因为φ(x)在[1,+∞]上单调递减,
-2x2,因为φ(x)在[1,+∞]上单调递减,
所以φ(x)max=φ(1)=0,所以a≥0.
(ⅱ)若函数g(x)为[1,+∞)上的单调减函数,则g′(x)≤0在[1,+∞)上恒成立,不可能.
综上,实数a的取值范围是[0,+∞).


科目:高中数学 来源: 题型:
【题目】已知![]() 为抛物线
为抛物线![]() :
: ![]() (
(![]() )的焦点,直线
)的焦点,直线![]() :
: ![]() 交抛物线
交抛物线![]() 于
于![]() ,
, ![]() 两点.
两点.
(Ⅰ)当![]() ,
, ![]() 时,求抛物线
时,求抛物线![]() 的方程;
的方程;
(Ⅱ)过点![]() ,
, ![]() 作抛物线
作抛物线![]() 的切线,
的切线, ![]() ,
, ![]() 交点为
交点为![]() ,若直线
,若直线![]() 与直线
与直线![]() 斜率之和为
斜率之和为![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如下表所示:
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中有1名男生的概率是多少?
(3)学生的学习积极性与对待班极工作的态度是否有关系?请说明理由.
附:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
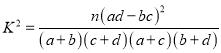
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“雅荷文学社”、“青春风街舞社”、“羽乒协会”、“演讲团”、“吉他协会”五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中至多有1人参加“演讲团”的不同参加方法数为( )
A. 4680 B. 4770 C. 5040 D. 5200
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位需要从甲、乙![]() 人中选拔一人参加新岗位培训,特别组织了
人中选拔一人参加新岗位培训,特别组织了![]() 个专项的考试,成绩统计如下:
个专项的考试,成绩统计如下:
第一项 | 第二项 | 第三项 | 第四项 | 第五项 | |
甲的成绩 |
|
|
|
|
|
乙的成绩 |
|
|
|
|
|
(1)根据有关统计知识,回答问题:若从甲、乙![]() 人中选出
人中选出![]() 人参加新岗培训,你认为选谁合适,请说明理由;
人参加新岗培训,你认为选谁合适,请说明理由;
(2)根据有关槪率知识,解答以下问题:
从甲、乙![]() 人的成绩中各随机抽取一个,设抽到甲的成绩为
人的成绩中各随机抽取一个,设抽到甲的成绩为![]() ,抽到乙的成绩为
,抽到乙的成绩为![]() ,用
,用![]() 表示满足条件
表示满足条件![]() 的事件,求事件
的事件,求事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率为
)的离心率为![]() ,连接椭圆的四个顶点得到的四边形的面积为
,连接椭圆的四个顶点得到的四边形的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的左焦点为
的左焦点为![]() ,右焦点为
,右焦点为![]() ,直线
,直线![]() 过点
过点![]() 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线![]() 垂直
垂直![]() 于点
于点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,求点
,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)设![]() 为坐标原点,取
为坐标原点,取![]() 上不同于
上不同于![]() 的点
的点![]() ,以
,以![]() 为直径作圆与
为直径作圆与![]() 相交另外一点
相交另外一点![]() ,求该圆面积的最小值时点
,求该圆面积的最小值时点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com