
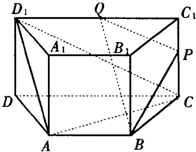
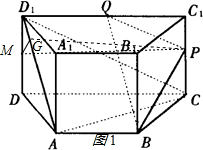
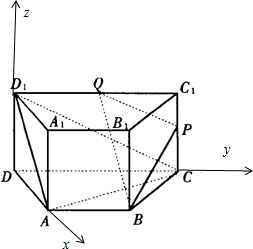
 如图,直四棱柱ABCD-A1B1C1D1的底面是梯形,AB∥CD,AD⊥DC,CD=2,DD1=AB=1,
如图,直四棱柱ABCD-A1B1C1D1的底面是梯形,AB∥CD,AD⊥DC,CD=2,DD1=AB=1,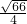 .
.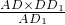 =
=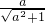
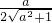
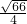
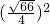 -
-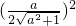 ,
,
 ),Q(0,1,1)
),Q(0,1,1) =(-1,1,
=(-1,1, ),
), =(0,-1,
=(0,-1, ),
), =(-1,2,0)
=(-1,2,0) =(x,y,z)
=(x,y,z)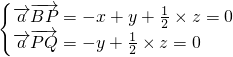
 =(2,1,2)
=(2,1,2)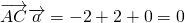
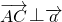 ,AC?平面BPQ
,AC?平面BPQ =(1,0,0)
=(1,0,0) =(2,1,2)
=(2,1,2) ,
, >=
>=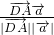 =
= =
=

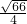 ,计算棱AD的长,由与AD⊥DC⊥DD1,所以以这三条棱为轴建立空间直角坐标系,写出相关点的坐标和相关向量的坐标,(1)先利用线面垂直的判定,求出平面BPQ的法向量
,计算棱AD的长,由与AD⊥DC⊥DD1,所以以这三条棱为轴建立空间直角坐标系,写出相关点的坐标和相关向量的坐标,(1)先利用线面垂直的判定,求出平面BPQ的法向量 ,再利用向量数量积运算证明AC垂直于平面BPQ的法向量,从而AC平行于平面BPQ,(2)先证明平面DPQ的法向量为
,再利用向量数量积运算证明AC垂直于平面BPQ的法向量,从而AC平行于平面BPQ,(2)先证明平面DPQ的法向量为 ,再结合(1),利用向量夹角公式计算两个法向量的夹角的余弦值即可的二面角的大小
,再结合(1),利用向量夹角公式计算两个法向量的夹角的余弦值即可的二面角的大小

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
 如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2.
如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8.| 1 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点.
(2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com