
【题目】已知函数![]() ,且
,且![]() .
.
(Ⅰ)若![]() 是关于
是关于![]() 的方程
的方程![]() 的一个解,求
的一个解,求![]() 的值;
的值;
(Ⅱ)当![]() 且
且![]() 时,解不等式
时,解不等式![]() ;
;
(Ⅲ)若函数![]() 在区间
在区间![]() 上有零点,求
上有零点,求![]() 的取值范围.
的取值范围.
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
【题目】某公司生产一种产品每年需投入固定成本为3万元,此外每生产1百件这种产品还需要增加投入1万元(总成本![]() 固定成本
固定成本![]() 生产成本).已知销售收入满足函数:
生产成本).已知销售收入满足函数: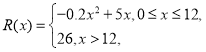 其中
其中![]() (百件)为年产量,假定该产品产销平衡(即生产的产品都能卖掉).
(百件)为年产量,假定该产品产销平衡(即生产的产品都能卖掉).
(1)请把年利润![]() 表示为当年生产量
表示为当年生产量![]() 的函数;(利润
的函数;(利润![]() 销售收入
销售收入![]() 总成本)
总成本)
(2)当年产量为多少百件时,公司所获利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级有50名学生,现要采取系统抽样的方法在这50名学生中抽出10名学生,将这50名学生随机编为1~50号,并进行分组,第一组1~5号,第二组6~10号,…,第十组46~50号.若在第三组中抽得号码为12的学生,则在第九组中抽得号码为_____的学生.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a1,d为实数,首项为a1,公差为d的等差数列{an}的前n项和为Sn,满足S5S6+15=0.
(1)若S5=5,求S6及a1;
(2)求d的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于直线的倾斜角与斜率,下列说法正确的是( )
A.所有的直线都有倾斜角和斜率
B.所有的直线都有倾斜角但不一定都有斜率
C.直线的倾斜角和斜率有时都不存在
D.所有的直线都有斜率,但不一定有倾斜角
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:
满足:![]() ,则称
,则称![]() 为“
为“![]() 函数”.
函数”.
(1)试判断![]() 是否为“
是否为“![]() 函数”,并说明理由;
函数”,并说明理由;
(2)若![]() 为“
为“![]() 函数”且
函数”且![]() ,
,
(ⅰ)求证:![]() 的零点在
的零点在![]() 上;
上;
(ii)求证:对任意![]() ,存在
,存在![]() ,使
,使![]() 在
在![]() 上恒成立.
上恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品按行业生产标准分成![]() 个等级,等级系数
个等级,等级系数![]() 依次
依次![]() ,其中
,其中![]() 为标准
为标准![]() ,
,![]() 为标准
为标准![]() .已知甲厂执行标准
.已知甲厂执行标准![]() 生产该产品,产品的零售价为
生产该产品,产品的零售价为![]() 元/件;乙厂执行标准
元/件;乙厂执行标准![]() 生产该产品,产品的零售价为
生产该产品,产品的零售价为![]() 元/件,假定甲、乙两厂的产品都符合相应的执行标准.
元/件,假定甲、乙两厂的产品都符合相应的执行标准.
(1)已知甲厂产品的等级系数![]() 的概率分布如下所示:
的概率分布如下所示:
|
|
|
|
|
|
|
|
|
|
且![]() 的数学期望
的数学期望![]() ,求
,求![]() 的值;
的值;
(2)为分析乙厂产品的等级系数![]() ,从该厂生产的产品中随机抽取
,从该厂生产的产品中随机抽取![]() 件,相应的等级系数组成一个样本,数据如下:
件,相应的等级系数组成一个样本,数据如下:

用这个样本的频率分布估计总体分布,将频率视为概率,求等级系数![]() 的数学期望;
的数学期望;
(3)在(1)、(2)的条件下,若以“性价比”为判断标准,则哪个工厂的产品更具可购买性?说明理由.注:①产品的“性价比”![]() ;
;
②“性价比”大的产品更具可购买性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com