
【题目】(1)讨论函数f(x)=![]() ex的单调性,并证明当x>0时,(x-2)ex+x+2>0.
ex的单调性,并证明当x>0时,(x-2)ex+x+2>0.
(2)证明:当a∈[0,1) 时,函数g(x)=![]() (x>0) 有最小值.设g(x)的最小值为h(a),求函数h(a)的值域.
(x>0) 有最小值.设g(x)的最小值为h(a),求函数h(a)的值域.
【答案】(1)在![]() 和
和![]() 上都是递增,证明见解析;(2)证明见解析,
上都是递增,证明见解析;(2)证明见解析,![]() .
.
【解析】试题分析:(1)求导后分析导数大于零(或小于零)的解,即可求出单调区间,利用极小值即可证明不等式成立;(2)利用二次求导求函数的单调性最值,从而求出h(a)的值域.
试题解析:
(1)f(x)=![]() ex,x∈(-∞,-2)∪(-2,+∞).
ex,x∈(-∞,-2)∪(-2,+∞).
f ′(x)=ex![]() =
=![]() ,
,
因为当x∈(-∞,-2)∪(-2,+∞)时,f ′(x)>0,
所以f(x)在(-∞,-2)和(-2,+∞)上单调递增,
所以x>0时,![]() ex>f(0)=-1,
ex>f(0)=-1,
所以(x-2)ex+x+2>0.
(2)g′(x)=![]()
=![]()
=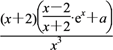 ,a∈[0,1).
,a∈[0,1).
由(1)知,当x>0时,f(x)=![]() ·ex的值域为(-1,+∞),只有一解,使得
·ex的值域为(-1,+∞),只有一解,使得![]() ·et=-a,t∈(0,2].
·et=-a,t∈(0,2].
当x∈(0,t)时g′(x)<0,g(x)单调递减;
当x∈(t,+∞)时g′(x)>0,g(x)单调递增.
h(a)=![]() =
=![]() =
=![]() ,
,
记k(t)=![]() ,在t∈(0,2]时,k′(t)=
,在t∈(0,2]时,k′(t)=![]() >0,
>0,
所以k(t)单调递增,
所以h(a)=k(t)∈![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别是双曲线
分别是双曲线![]() 的左顶点、右焦点,过
的左顶点、右焦点,过![]() 的直线
的直线![]() 与
与![]() 的一条渐近线垂直且与另一条渐近线和
的一条渐近线垂直且与另一条渐近线和![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.若
两点.若![]() ,则
,则![]() 的离心率是( )
的离心率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于x的方程2x2﹣ax﹣2=0的两根分别为α、β(α<β),函数![]()
(1)证明f(x)在区间(α,β)上是增函数;
(2)当a为何值时,f(x)在区间[α,β]上的最大值与最小值之差最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家具公司制作木质的椅子和书桌两种家具,需要木工和漆工两道工序,已知木工平均6个小时做一把椅子,10个小时做一张书桌,该公司每月木工最多有6000个工作时;漆工平均4个小时漆一把椅子,2个小时漆一张书桌,该公司每月漆工最多有2600个工作时![]() 又已知制作一把椅子和一张书桌的利润分别是15元和20元,根据以上条件,怎样安排每月的生产,才能获得最大的利润?
又已知制作一把椅子和一张书桌的利润分别是15元和20元,根据以上条件,怎样安排每月的生产,才能获得最大的利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() lnx-x+
lnx-x+![]() ,其中a>0.
,其中a>0.
(1)若f(x)在(0,+∞)上存在极值点,求a的取值范围;
(2)设a∈(1,e],当x1∈(0,1),x2∈(1,+∞)时,记f(x2)-f(x1)的最大值为M(a).那么M(a)是否存在最大值?若存在,求出其最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构为了了解各年龄层对高考改革方案的关注程度,随机选取了200名年龄在![]() 内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为
内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
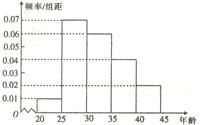
(1)求选取的市民年龄在![]() 内的人数;
内的人数;
(2)若从第3,4组用分层抽样的方法选取5名市民进行座谈,再从中选取2人在座谈会中作重点发言,求作重点发言的市民中至少有一人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:已知函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,若
,若![]() 恒成立,则称函数
恒成立,则称函数![]() 在
在![]() 上具有“
上具有“![]() ”性质.
”性质.
(![]() )判断函数
)判断函数![]() 在
在![]() 上是否具有“
上是否具有“![]() ”性质?说明理由.
”性质?说明理由.
(![]() )若
)若![]() 在
在![]() 上具有“
上具有“![]() ”性质,求
”性质,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com