
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以原点
为参数).在以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】分析:解法一:(1)消去参数可得![]() 的普通方程为
的普通方程为![]() ,则极坐标方程为
,则极坐标方程为![]() .极坐标方程化为直角坐标方程可得
.极坐标方程化为直角坐标方程可得![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)设![]() 的极坐标分别为
的极坐标分别为![]() ,则
,则![]() ,联立极坐标方程可得
,联立极坐标方程可得![]() , 则
, 则![]() ,结合三角函数的性质计算可得
,结合三角函数的性质计算可得![]() .
.
解法二: (1)同解法一
(2)曲线![]() 表示圆心为
表示圆心为![]() 且半径为1的圆.联立直线参数方程的标准形式与圆的方程可得
且半径为1的圆.联立直线参数方程的标准形式与圆的方程可得![]() ,结合参数的几何意义知
,结合参数的几何意义知![]() , 则
, 则![]()
解法三: (1)同解法一
(2)曲线![]() 表示圆心为
表示圆心为![]() 且半径为1的圆.
且半径为1的圆. ![]() 的普通方程为
的普通方程为![]() , 由弦长公式可得
, 由弦长公式可得![]() ,则
,则![]() 是等边三角形,
是等边三角形,![]() ,
, ![]() .
.
详解:解法一:(1)由![]() 得
得![]() 的普通方程为
的普通方程为![]() ,
,
又因为![]() , 所以
, 所以![]() 的极坐标方程为
的极坐标方程为![]() .
.
由![]() 得
得![]() ,即
,即![]() ,
,
所以![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)设![]() 的极坐标分别为
的极坐标分别为![]() ,则
,则![]()
由![]() 消去
消去![]() 得
得![]() ,
,
化为![]() ,即
,即![]() ,
,
因为![]() ,即
,即![]() ,所以
,所以![]() ,或
,或![]() ,
,
即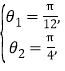 或
或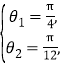 所以
所以![]() .
.
解法二: (1)同解法一
(2)曲线![]() 的方程可化为
的方程可化为![]() ,表示圆心为
,表示圆心为![]() 且半径为1的圆.
且半径为1的圆.
将![]() 的参数方程化为标准形式
的参数方程化为标准形式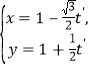 (其中
(其中![]() 为参数),代入
为参数),代入![]() 的直角坐标方程为
的直角坐标方程为![]() 得,
得,![]() ,
,
整理得,![]() ,解得
,解得![]() 或
或![]() .
.
设![]() 对应的参数分别为
对应的参数分别为![]() ,则
,则![]() .所以
.所以![]() ,
,
又因为![]() 是圆
是圆![]() 上的点,所以
上的点,所以![]()
解法三: (1)同解法一
(2)曲线![]() 的方程可化为
的方程可化为![]() ,表示圆心为
,表示圆心为![]() 且半径为1的圆.
且半径为1的圆.
又由①得![]() 的普通方程为
的普通方程为![]() ,
,
则点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以![]() ,所以
,所以![]() 是等边三角形,所以
是等边三角形,所以![]() ,
,
又因为![]() 是圆
是圆![]() 上的点,所以
上的点,所以![]() .
.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,底面ABCD是正方形,AC与BD交于点O,
中,底面ABCD是正方形,AC与BD交于点O,![]() 底面ABCD,F为BE的中点,
底面ABCD,F为BE的中点,![]() .
.
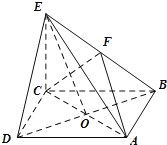
(1)求证:![]() 平面ACF;
平面ACF;
(2)求BE与平面ACE的所成角的正切值;
(3)在线段EO上是否存在点G,使CG![]() 平面BDE ?若存在,求出EG:EO的值,若不存在,请说明理由.
平面BDE ?若存在,求出EG:EO的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c∈(0,+∞).
(1)若a=6,b=5,c=4是△ABC边BC,CA,AB的长,证明:cosA∈Q;
(2)若a,b,c分别是△ABC边BC,CA,AB的长,若a,b,c∈Q时,证明:cosA∈Q;
(3)若存在λ∈(-2,2)满足c2=a2+b2+λab,证明:a,b,c可以是一个三角形的三边长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,曲线C由上半椭圆C1: ![]() =1(a>b>0,y≥0)和部分抛物线C2:y=﹣x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1的离心率为
=1(a>b>0,y≥0)和部分抛物线C2:y=﹣x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1的离心率为 ![]() .
. 
(1)求a,b的值;
(2)过点B的直线l与C1 , C2分别交于点P,Q(均异于点A,B),若AP⊥AQ,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分别直方图.
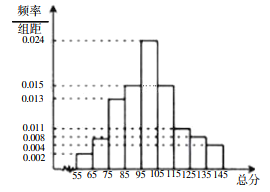
(1)求这100份数学试卷成绩的中位数;
(2)从总分在![]() 和
和![]() 的试卷中随机抽取2份试卷,求抽取的2份试卷中至少有一份总分少于65分的概率.
的试卷中随机抽取2份试卷,求抽取的2份试卷中至少有一份总分少于65分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com